
Answer
403.4k+ views
Hint: Polarizing angle is defined as an angle of incidence at which light with a particular polarization is perfectly transmitted through a transparent dielectric surface. In optics, the smallest angle of incidence that causes total internal reflection of light is known as Critical angle. Now, use the formula for polarizing angle in terms of critical angle. Rearrange the equation and using trigonometric function find the relation between polarizing angle and critical angle.
Formula used:
$\tan { \left( { i }_{ p } \right) } = \dfrac { 1 }{ \sin { \left( { \theta }_{ c } \right) } }$
Complete solution step-by-step:
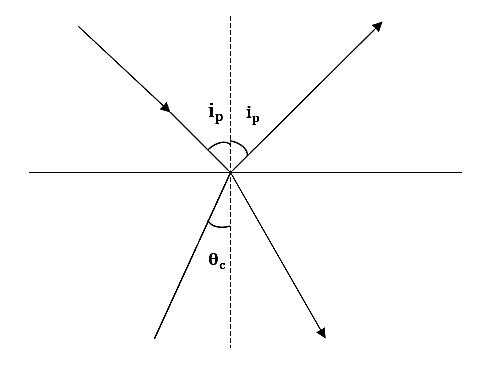
Let the polarizing angle be ${i}_{p}$
The critical angle be ${ \theta }_{ c }$
The relation between critical angle and polarizing angle is given by,
$\tan { \left( { i }_{ p } \right) } = \dfrac { 1 }{ \sin { \left( { \theta }_{ c } \right) } }$ …(1)
We know,
$\csc { { \theta }_{ c } } = \dfrac { 1 }{ \sin { \left( { \theta }_{ c } \right) } }$ …(2)
Substituting equation. (2) in equation. (1) we get,
$\tan { \left( { i }_{ p } \right) } =\csc { { \theta }_{ c } }$
Rearranging the above equation we get,
${ i }_{ p }=\tan ^{ -1 }{{ \left( \csc { { \theta }_{ c } } \right) }}$
Thus, the relation between the polarizing angle and the critical angle is
${ i }_{ p }=\tan ^{ -1 }{{ \left( \csc { { \theta }_{ c } } \right) }}$.
So, the correct answer is option A i.e. ${ i }_{ p }=\tan ^{ -1 }{{ \left( \csc { { \theta }_{ c } } \right) }}$.
Note:
Students must remember that the polarizing angle is also known as Brewster’s angle. When the light strikes at Brewster’s angle, the reflected ray and the refracted ray will be perpendicular to each other and the reflected ray will be linearly polarized. The incident ray will not be polarized. It is temporarily absorbed by the medium. Polarized sunglasses use the principle of Brewster’s angle to reduce the glare from the sun reflecting off horizontal surfaces such as water on the road.
Formula used:
$\tan { \left( { i }_{ p } \right) } = \dfrac { 1 }{ \sin { \left( { \theta }_{ c } \right) } }$
Complete solution step-by-step:

Let the polarizing angle be ${i}_{p}$
The critical angle be ${ \theta }_{ c }$
The relation between critical angle and polarizing angle is given by,
$\tan { \left( { i }_{ p } \right) } = \dfrac { 1 }{ \sin { \left( { \theta }_{ c } \right) } }$ …(1)
We know,
$\csc { { \theta }_{ c } } = \dfrac { 1 }{ \sin { \left( { \theta }_{ c } \right) } }$ …(2)
Substituting equation. (2) in equation. (1) we get,
$\tan { \left( { i }_{ p } \right) } =\csc { { \theta }_{ c } }$
Rearranging the above equation we get,
${ i }_{ p }=\tan ^{ -1 }{{ \left( \csc { { \theta }_{ c } } \right) }}$
Thus, the relation between the polarizing angle and the critical angle is
${ i }_{ p }=\tan ^{ -1 }{{ \left( \csc { { \theta }_{ c } } \right) }}$.
So, the correct answer is option A i.e. ${ i }_{ p }=\tan ^{ -1 }{{ \left( \csc { { \theta }_{ c } } \right) }}$.
Note:
Students must remember that the polarizing angle is also known as Brewster’s angle. When the light strikes at Brewster’s angle, the reflected ray and the refracted ray will be perpendicular to each other and the reflected ray will be linearly polarized. The incident ray will not be polarized. It is temporarily absorbed by the medium. Polarized sunglasses use the principle of Brewster’s angle to reduce the glare from the sun reflecting off horizontal surfaces such as water on the road.



