Question

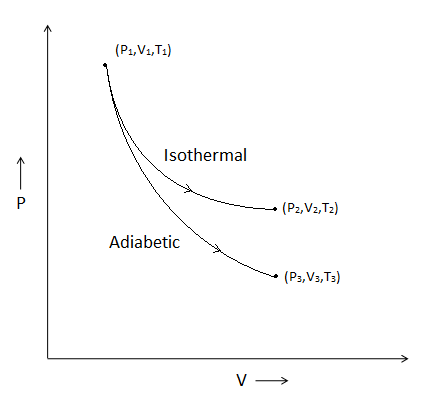
The reversible expansion of an ideal gas under adiabatic and isothermal conditions is shown in the figure. Which of the following statement(s) is(are) correct?

[This question has multiple correct options]
(A) ${T_1} = {T_2}$
(B) ${T_3} > {T_1}$
(C) ${w_{isothermal}} > {w_{adiabatic}}$
(D) $\Delta {U_{isothermal}} > \Delta {U_{adiabatic}}$

Answer 1

Hint: Isothermal process is a process in which the temperature remains the same throughout the process. So, $\Delta T = 0$. In adiabatic processes, the heat of the system remains constant, so $\Delta Q = 0$ .

Complete answer:
We will find which of the statements are wrong as given in the graph.
- Isothermal process is a process in which the temperature remains the same throughout the process. In the isothermal curve, we can see that the initial temperature is ${T_1}$ and the final temperature is ${T_2}$. We know that as the process is isothermal, the temperature will not change. Thus, we can say that ${T_1} = {T_2}$.
- In adiabatic processes, the heat of the system remains constant. So, in this process, we can say that the initial temperature is shown as ${T_1}$ in the adiabatic curve. The final temperature is ${T_3}$. We can say that the final temperature is lower than the initial temperature from the curve. Thus, ${T_1} > {T_3}$.
- In the isothermal process, we know that $\Delta {U_{isothermal}}$ is zero. Thus, we can say that this energy gets converted into work (${w_{isothermal}}$) done. For adiabatic process, Q = 0. Thus, we can say that the work done by the isothermal process will be higher than the adiabatic process. So, ${w_{isothermal}} > {w_{adiabatic}}$
- We have seen earlier that the change in internal energy in isothermal energy is zero. Thus, $\Delta {U_{isothermal}} = 0$ . But in adiabatic processes, the work done is always negative. So, we can say that $\Delta {U_{isothermal}} > \Delta {U_{adiabatic}}$

Thus, we can conclude that options (A), (C) and (D) are correct.

Note:
Remember that a process can be called reversible if the change is brought in such a way that it can be reversed by a change. It involves equilibrium states in it. The processes that are not reversible are called irreversible processes.