Question

The shadow of a tower standing on level ground is found to be 40 m longer when the Sun’s altitude is \[{{30}^{\circ }}\] than when it was \[{{60}^{\circ }}.\] Find the height of the tower. \[\left( \text{Given }\sqrt{3}=1.732 \right)\]

Answer 1

Hint: To solve the given question, we will assume that the height of the tower is h. Then, we will assume that when the sun’s altitude is \[{{30}^{\circ }},\] the length of the shadow of the building is x and when the sun’s altitude is \[{{60}^{\circ }},\] the length of the shadow of the building on the ground is y. Then, we will develop a relation between x and y using the information given in the question that the difference in x and y is 40 m. Now, we will apply trigonometry in the triangle formed by the length of the shadow when the sun's altitude is \[{{30}^{\circ }}\] and the height of the building as h.

Complete step-by-step answer:
To start with, we are going to first draw a rough sketch. In this, we are considering the length of the shadow on level ground as x when the sun’s altitude is \[{{30}^{\circ }}\] and the length of shadow as y when the sun’s altitude is \[{{60}^{\circ }}.\] The height of the tower is h.

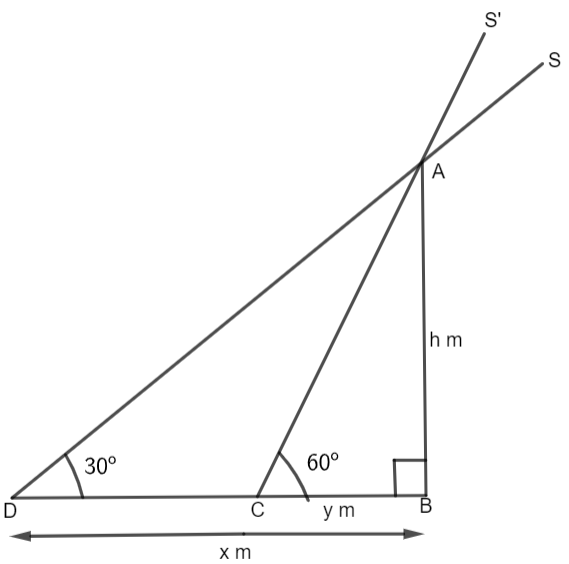
In the figure, BC and BD are the lengths of the shadows when the sun’s altitude is \[{{60}^{\circ }}\] and \[{{30}^{\circ }}\] respectively. AB is the height of the building. S and S’ are positions of the sun. Now, it is given in the question that the difference in length of shadows is 40m. Thus, we will get,
\[x-y=40m.....\left( i \right)\]
Now, we will consider the right-angled triangle ABD. We know that in any right-angled triangle the ratio of the perpendicular to the base is given by tan of the angle between the hypotenuse and the base. Thus, we can say that,
\[\tan D=\dfrac{AB}{BD}\]
\[\Rightarrow \tan {{30}^{\circ }}=\dfrac{h}{x}\]
Now, the value of \[\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}.\] So, we have,
\[\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{h}{x}\]
\[\Rightarrow x=h\sqrt{3}.....\left( ii \right)\]
Now, we will consider the right-angled triangle ABC. In this triangle, BC is the base and AB is the perpendicular. So, we have,
\[\tan C=\dfrac{AB}{BC}\]
\[\Rightarrow \tan {{60}^{\circ }}=\dfrac{h}{y}\]
Now, the value of \[\tan {{60}^{\circ }}=\sqrt{3}.\] So, we have,
\[\Rightarrow \sqrt{3}=\dfrac{h}{y}\]
\[\Rightarrow y=\dfrac{h}{\sqrt{3}}.....\left( iii \right)\]
Now, we will put the values of x and y from (ii) and (iii) to (i). Thus, we will get,
\[\Rightarrow h\sqrt{3}-\dfrac{h}{\sqrt{3}}=40m\]
\[\Rightarrow \dfrac{\sqrt{3}\left( h\sqrt{3} \right)-h}{\sqrt{3}}=40m\]
\[\Rightarrow \dfrac{3h-h}{\sqrt{3}}=40m\]
\[\Rightarrow \dfrac{2h}{\sqrt{3}}=40m\]
\[\Rightarrow h=20\sqrt{3}m\]
\[\Rightarrow h=20\times 1.732=34.64m\]
Thus, the height of the building is 34.64 m.

Note: While solving the question, we have assumed that the building is perfectly perpendicular to the ground level. Also, we have assumed the building as a straight line and not as a 3D object because in 3D, the shadow of each dimension of the building would be different and we are not given this much information to solve the question by considering 3 dimensions of the building.