Question

The shortest distance between the parabola ${y^2} = 4x$ and the circle ${x^2} + {y^2} + 6x - 12y + 20 = 0$ is
$\left( a \right)4\sqrt 2 - 5$
$\left( b \right)0$
$\left( c \right)3\sqrt 2 + 5$
$\left( d \right)1$

Answer 1

Hint: In this particular question use the concept that the shortest distance between the parabola and the circle is the difference of the perpendicular drawn from the center of the circle on the parabola and the radius of the circle, so use this concept to reach the solution of the question.

Complete step-by-step answer:

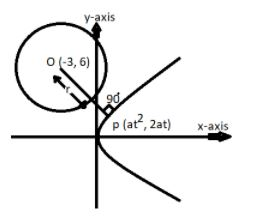
Given equation of circle is
${x^2} + {y^2} + 6x - 12y + 20 = 0$
Now make the complete square in x and y by adding and subtracting by the half the square of the coefficient of x and y respectively.
$ \Rightarrow {x^2} + {y^2} + 6x + {\left( {\dfrac{6}{2}} \right)^2} - {\left( {\dfrac{6}{2}} \right)^2} - 12y + {\left( {\dfrac{{12}}{2}} \right)^2} - {\left( {\dfrac{{12}}{2}} \right)^2} + 20 = 0$
$ \Rightarrow {x^2} + 6x + 9 + {y^2} - 12y + 36 = 36 + 9 - 20$
$ \Rightarrow {\left( {x + 3} \right)^2} + {\left( {y - 6} \right)^2} = 25 = {5^2}$
Now compare with standard equation of circle which is given as,
$ \Rightarrow {\left( {x - g} \right)^2} + {\left( {y - f} \right)^2} = {r^2}$, where (g, f) and r is the center and the radius of the circle respectively.
So on comparing the center of the given circle = (-3, 6) and radius, r = 5.
Now the equation of the given parabola is ${y^2} = 4x$.
As the standard equation of parabola is , ${y^2} = 4ax$
So on comparing, 4a = 4.
Therefore, a =1.
Now as we all know that the parametric coordinate (p) of the parabola is $\left( {a{t^2},2at} \right)$
Now substitute the value of a in the above coordinates, so the parametric coordinate is, p = $\left( {{t^2},2t} \right)$.
Now as we know that the equation of the normal through the parametric coordinate p on the parabola is given as,
$y = - tx + 2at + a{t^3}$
Now substitute the value of a in the above equation we have,
$ \Rightarrow y = - tx + 2t + {t^3}$............... (1)
Now as we know that the shortest distance between the parabola and the circle is the difference of the perpendicular drawn from the center of the circle on the parabola and the radius of the circle.
So in order to calculate the shortest distance equation (1) must be passed through the center of the circle.
So satisfy the coordinate of circle (-3, 6) in equation (1) we have,
$ \Rightarrow 6 = 3t + 2t + {t^3}$
$ \Rightarrow {t^3} + 5t - 6 = 0$
So when we substitute t =1 the equation become,
1 + 5 – 6 = 0
6 – 6 = 0
 0 = 0
So t = 1 is the root of the cubic equation.
So (t – 1) is the factor of the cubic equation.
Let the other factor be ($a{t^2} + bt + c$)
So the first factor multiplied by this factor gives the resultant cubic equation.
Therefore, ${t^3} + 5t - 6 = \left( {a{t^2} + bt + c} \right)\left( {t - 1} \right)$
$ \Rightarrow {t^3} + 5t - 6 = \left( {a{t^3} + \left( {b - a} \right){t^2} + \left( {c - b} \right)t - c} \right)$
Now on comparing we have,
a = 1,
b – a = 0 .................. (2)
c – b = 5 .................. (3)
And, c = 6
Substitute the value of a in any above equation we have,
Therefore, b – 1 = 0
Therefore, b = 1.
So the other factor of the equation is, $\left( {{t^2} + t + 6} \right)$
So the cubic equation become
$ \Rightarrow {t^3} + 5t - 6 = \left( {{t^2} + t + 6} \right)\left( {t - 1} \right)$
Now the discriminant of the other factor of the cubic equation is,
$ \Rightarrow D = {b^2} - 4ac = {1^2} - 4\left( 1 \right)\left( 6 \right) = 1 - 24 = - 23$
So as we see that discriminant, D is less than zero.
So the other roots of the equation are complex.
So there is only one possible value of t, which is 1.
So the parametric coordinate become, $\left( {{t^2},2t} \right)$ = (1, 2)
Now as we know that the distance (d) between two points $\left( {{x_1},{y_1}} \right){\text{ and }}\left( {{x_2},{y_2}} \right)$ is
$ \Rightarrow d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $
So the distance between parametric coordinate (1, 2) and the center of the circle (-3, 6) is
Let, (1, 2) = $\left( {{x_1},{y_1}} \right)$
And (-3, 6) = $\left( {{x_2},{y_2}} \right)$
$ \Rightarrow d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $
$ \Rightarrow d = \sqrt {{{\left( { - 3 - 1} \right)}^2} + {{\left( {6 - 2} \right)}^2}} $
$ \Rightarrow d = \sqrt {{{\left( { - 4} \right)}^2} + {{\left( 4 \right)}^2}} $
$ \Rightarrow d = \sqrt {16 + 16} = \sqrt {32} = 4\sqrt 2 $
So the shortest distance between the parabola and the circle = d – r
$ \Rightarrow 4\sqrt 2 - 5$
So this is the required shortest distance.

So, the correct answer is “Option A”.

Note: Whenever we face such types of questions the key concept we have to remember is that the equation of the normal through the parametric coordinate p ($a{t^2},2at$) on the parabola (${y^2} = 4ax$) is given as, $y = - tx + 2at + a{t^3}$, and the distance (d) between two points $\left( {{x_1},{y_1}} \right){\text{ and }}\left( {{x_2},{y_2}} \right)$ is given as $d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} $.