
The S.I unit of magnetic moment is ________.
Answer
434k+ views
1 likes
Hint: The magnetic moment of a bar magnet is defined as the product of one of the pole strengths with the distance between the poles (magnetic length). It’s a vector quantity and conventionally its direction taken from S- pole to N- pole.
Formulas used:
The magnetic dipole moment of a magnet having pole strength
Torque on a magnetic dipole in a magnetic field with strength
Complete step by step answer:
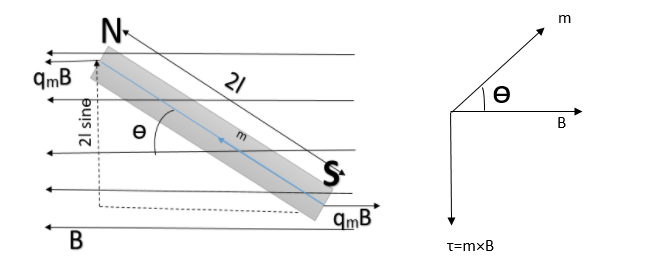
Consider a bar magnet of length
Force on North-pole is
Force on South-pole is
The force on the two poles are equal and opposite, they form a couple, moment of couple or torque is given by
Where
In vector form the torque is written as
Unit of magnetic moment:
The S.I unit of
So S.I unit of magnetic moment is
Additional Information:
The direction of torque is perpendicular to the plane containing both the magnet and the magnetic field. The effect of the torque is to make the magnet align itself parallel to the external magnetic field. Due to this a freely suspended magnet aligns itself in the north south direction.
Note:
When the angle between the magnetic axis and the external field is zero i.e.
When the magnet lies perpendicular to the field then
Formulas used:
The magnetic dipole moment of a magnet having pole strength
Torque on a magnetic dipole in a magnetic field with strength
Complete step by step answer:

Consider a bar magnet of length
Force on North-pole is
Force on South-pole is
The force on the two poles are equal and opposite, they form a couple, moment of couple or torque is given by
Where
In vector form the torque is written as
Unit of magnetic moment:
The S.I unit of
So S.I unit of magnetic moment is
Additional Information:
The direction of torque is perpendicular to the plane containing both the magnet and the magnetic field. The effect of the torque is to make the magnet align itself parallel to the external magnetic field. Due to this a freely suspended magnet aligns itself in the north south direction.
Note:
When the angle between the magnetic axis and the external field is zero i.e.
When the magnet lies perpendicular to the field then
Latest Vedantu courses for you
Grade 8 | CBSE | SCHOOL | English
Vedantu 8 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




