Question

The side length of an equilateral triangle is 20 cm. How do you find the length of the altitude of the triangle?

Answer 1

Hint: First of all we draw a diagram of the triangle and also draw its altitude. We use the fact that all sides of an equilateral triangle are equal in measure. Then we will use the Pythagoras theorem to find the length of the altitude.

Complete step-by-step solution:
We have been given that the side length of an equilateral triangle is 20 cm.
We have to find the length of the altitude of the triangle.
First let us draw a triangle $\Delta ABC$ and also draw its altitude AD. We will get

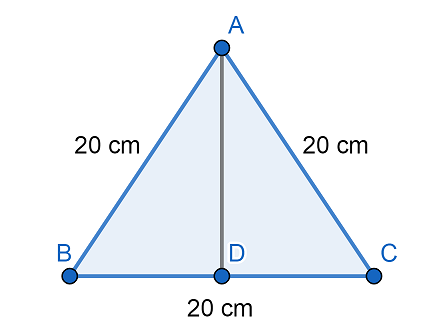
We know that an altitude divides an equilateral triangle into two right-triangles.
By Pythagoras theorem we know that ${{\left( \text{Hypotenuse} \right)}^{2}}={{\left( \text{Base} \right)}^{2}}+{{\left( \text{Perpendicular} \right)}^{2}}$
Now, let us consider right triangle $\Delta ABD$, we will get
${{\left( AB \right)}^{2}}={{\left( BD \right)}^{2}}+{{\left( AD \right)}^{2}}$
Now, we have $AB=20cm$ and $BD=10cm$ (as altitude divides the base into two equal halves)
Now, substituting the values we will get
$\Rightarrow {{\left( 20 \right)}^{2}}={{\left( 10 \right)}^{2}}+{{\left( AD \right)}^{2}}$
Now, simplifying further the above obtained equation we will get
$\begin{align}
  & \Rightarrow {{\left( 20 \right)}^{2}}={{\left( 10 \right)}^{2}}+{{\left( AD \right)}^{2}} \\
 & \Rightarrow 400=100+A{{D}^{2}} \\
 & \Rightarrow 400-100=A{{D}^{2}} \\
 & \Rightarrow 300=A{{D}^{2}} \\
 & \Rightarrow AD=\sqrt{300} \\
 & \Rightarrow AD=17.3\text{ cm} \\
\end{align}$
So we get the length of the altitude as $17.3\text{ cm}$.

Note: Alternatively we can use trigonometric ratio to find the length of the altitude. As we know that all angles of an equilateral triangle measures $60{}^\circ $.
Let us consider $\Delta ABD$, assume that $\angle ABD=60{}^\circ $.
So we know that $\sin 60{}^\circ =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$
Substituting the values and solving further we will get
$\begin{align}
  & \Rightarrow \sin 60{}^\circ =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}} \\
 & \Rightarrow \sin 60{}^\circ =\dfrac{AD}{AB} \\
\end{align}$
We know that by trigonometric table we have $\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}$.
Substituting the value and solving further we will get
\[\begin{align}
  & \Rightarrow \dfrac{\sqrt{3}}{2}=\dfrac{AD}{20} \\
 & \Rightarrow \dfrac{\sqrt{3}}{2}\times 20=AD \\
 & \Rightarrow 10\sqrt{3}=AD \\
 & \Rightarrow AD=17.3\text{ cm} \\
\end{align}\]