Question

The side of an isosceles right triangle of hypotenuse \[5\sqrt 2 \] cm is:
A. \[10\] cm
B. \[8\] cm
C. \[5\] cm
D. \[3\sqrt 2 \] cm

Answer 1

Hint: An isosceles triangle is a triangle that has two sides of equal length sometimes it is specified as having exactly two sides of equal length and sometimes as having at least two side of equal length the isosceles triangle includes the isosceles right triangle.
                                        

ABC is an isosceles triangle whose side AB\[ = \]BC.

Isosceles right triangle:

                                   

Sides other than hypotenuse of an isosceles triangle are equal.


Complete step-by- step solution-:
Given data,
Hypotenuse of an isosceles right triangle is \[5\sqrt 2 \] cm.
\[\therefore \] Sides other than Hypotenuse of an isosceles triangle are equal.
Let the other two Sides be \[x\] each

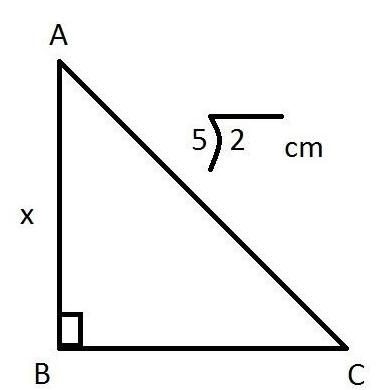
Using Pythagoras Theorem we know that
\[A{B^2} + B{C^2} = A{C^2}\] …….. (i)
i.e. \[{(Perpendicular)^2} + {(Base)^2} = {(Hypotenuse)^2}\]
Putting values \[AB = x = BC\] and \[AB = 5\sqrt 2 \] cm in the equation(i) we get
\[{x^2} + {x^2} = {(5\sqrt 2 )^2}\] \[[\therefore \sqrt 2 \times \sqrt 2 = 2\,\,\,i.e.\,\,{(\sqrt 2 )^2} = 2]\]
\[2{x^2} = 25 \times 2\]
\[{x^2} = 25\]
\[x = \sqrt {25} \]
\[x = \sqrt {5 \times 5} \]
\[x = 5\] [Square root of \[25\] is \[5\].]

So, the required side of an isosceles triangle is \[5\]cm each. Option C

Note:
Pythagoras theorem states that “In a right-angled triangle, the square of the hypotenuse side is equal to the sum of squares of the other two sides “. The sides of this triangle have been named as Perpendicular, Base and Hypotenuse.
Pythagoras is a theorem which is used only for right angled triangles.
Which is,
\[{(Perpendicular)^2} + {(Base)^2} = {(Hypotenuse)^2}\] [Remember]
Square root of a number is a value that, when multiplied by itself, gives the number i.e. \[\sqrt {25} = \sqrt {5 \times 5} = 5\]