Question

The sides of a triangle are 5, 12, 13 then its area.

Answer 1

Hint:
If we know the length sides of the triangle then we can calculate the area of the triangle by the formula called heron’s formula. The heron’s formula is given by
$ \Rightarrow A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $
Where A is the area of triangle; a, b and c are the sides of a triangle and s is the half the perimeter of the triangle i.e.
\[ \Rightarrow s = \dfrac{{a + b + c}}{2}\]

Complete step by step solution:
Let us see what is given to us? In this question all the three sides are given to us i.e.
$ \Rightarrow a = 5$, $b = 12$ and $c = 13$ ………..(1)

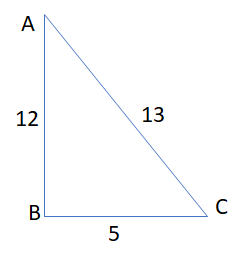
We have to find the area of the triangle.
To find the area of triangle we can use heron’s formula as we know all the three sides by formula:
$ \Rightarrow A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $ ………….(2)
To calculate the area, we need to find the value of s i.e.
\[ \Rightarrow s = \dfrac{{a + b + c}}{2}\]
Put the value of a, b and c from (1), we get,
\[ \Rightarrow s = \dfrac{{5 + 12 + 13}}{2}\]
By adding the numbers in numerator, we get,
$ \Rightarrow s = \dfrac{{30}}{2}$
By dividing 2 with 30, we get,
$ \Rightarrow s = 15$ ………….(3)
Put the values of (1) and (3) in (2) and we get,
$ \Rightarrow A = \sqrt {15\left( {15 - 5} \right)\left( {15 - 12} \right)\left( {15 - 13} \right)} $
Using BODMAS rule, first we will solve the brackets and we get,
$ \Rightarrow A = \sqrt {15\left( {10} \right)\left( 3 \right)\left( 2 \right)} $
By multiplying each number inside the square root, we get,
$ \Rightarrow A = \sqrt {900} $
As the square of 30 is 900. Therefore, the square root of 900 is 30 and we get,
 $ \Rightarrow A = 30$ ……………(4)

So, the area of the triangle is 30.

Note:
Alternate method:
In this question by analysing the length of the side it is noted that they form Pythagorean triplets i.e. they satisfy the Pythagoras theorem i.e.
$ \Rightarrow {c^2} = {a^2} + {b^{^2}}$
So, it is a right-angle triangle with a and b are sides & c is the hypotenuse. So, area of triangle of right-angle triangle is given by,
$ \Rightarrow A = \dfrac{1}{2} \times a \times b$
Putting value of a and b from (1) and we get,
$ \Rightarrow A = \dfrac{1}{2} \times 5 \times 12$
By cancelling 12 with 2, we get,
$ \Rightarrow A = 5 \times 6$
$ \Rightarrow A = 30$ ……………(5)
By comparing (4) and (5), It is noted by using any method we can get the same answer but for that sides of triangles should form Pythagorean triplets.