Question

The sides of a triangle are in the ratio 2:3:4. If its perimeter is 54 cm, find the lengths of the sides of the triangle

Answer 1

Hint: The perimeter of a triangle is the sum of lengths of its sides. Here the sides can be taken 2x, 3x and 5x respectively and added. The sum would be equal to the given perimeter and on solving the equation we can find the value of x. Then, the sides can be found accordingly.

Complete step-by-step answer:
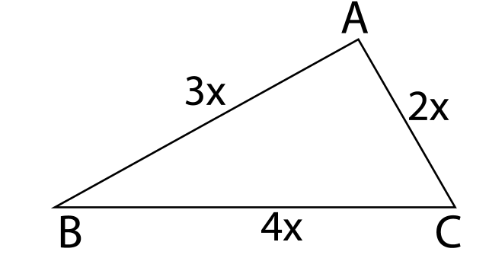
Let the given triangle be ABC is drawn below.

Whenever you are comparing two numbers, it becomes necessary to find out how many times is the one number greater than the other number. You can say that in other words, we need to express one number as a fraction of the other number.
Now, because the sides are given in ratio, we can assume them to be multiples of a constant number. Let the sides in ratio 2:3:4 be 2x, 3x and 4x respectively as follows.
So, according to the diagram
AB= 3x
BC= 4x
CA= 2x
Now, the perimeter of a polygon/shape is the sum of lengths of all its sides. So here,
Perimeter= length of side AB + length of side BC + length of side CA
 $
  P = AB + BC + CA \\
   \Rightarrow P = 3x + 4x + 2x \\
   \Rightarrow P = 9x \;
  $
Where P is the perimeter of the triangle.
According to the question, we are given that the perimeter of the triangle is 54 cm. So on substituting the value of perimeter in above equation,
 $
   \Rightarrow 54\;cm = 9x \\
   \Rightarrow x = \dfrac{{54}}{9}\;cm \\
   \Rightarrow x = 6\;cm \;
  $
Now, we can find the respective sides using the value of x and substituting it in the assumed values.
 $
  AB = 3x = 3 \times 6 = 18\;cm \\
  BC = 4x = 4 \times 6 = 24\;cm \\
  CA = 2x = 2 \times 6 = 12\;cm \;
  $
Therefore, the correct answer is 12 cm, 18 cm and 24 cm.
So, the correct answer is “12 cm, 18 cm and 24 cm”.

Note: For any questions relating to the area or perimeter of certain shapes/ polygons, it is helpful to draw diagrams before solving the questions. Also, for this question we can directly make the equations as
 $ 54 = 2x + 3x + 4x $ instead of doing it in two steps. One common mistake that has to be avoided here is that students leave the solution after finding the constant, and do not proceed to find the lengths of sides.