Question

The sides of a triangle inscribed in a given circle subtend angle $\alpha ,\beta $ and $\gamma $ at the center. The minimum value of the arithmetic means of $\cos \left( \alpha +\dfrac{\pi }{2} \right),\cos \left( \beta +\dfrac{\pi }{2} \right)$ and $\cos \left( \gamma +\dfrac{\pi }{2} \right)$ is equal to

A. 0
B. $\dfrac{1}{\sqrt{2}}$
C. $-1$
D. $-\dfrac{\sqrt{3}}{2}$

Answer 1

Hint: To find the arithmetic means of $\cos \left( \alpha +\dfrac{\pi }{2} \right),\cos \left( \beta +\dfrac{\pi }{2} \right)$ and $\cos \left( \gamma +\dfrac{\pi }{2} \right)$, we will add them and divide the sum by 3. We will use the property that the sum of angles subtended at the center of the circle is $360{}^\circ $. Then by simplifying the obtained equations we will get the desired answer.

Complete step by step answer:
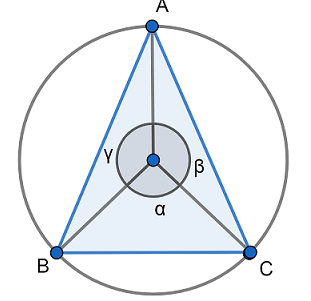
We have been given that the sides of a triangle inscribed in a given circle subtend angle $\alpha ,\beta $ and $\gamma $ at the center.

We have to find the minimum value of the arithmetic means of $\cos \left( \alpha +\dfrac{\pi }{2} \right),\cos \left( \beta +\dfrac{\pi }{2} \right)$ and $\cos \left( \gamma +\dfrac{\pi }{2} \right)$.
Now, as seen in the figure the angles $\alpha ,\beta $ and $\gamma $ subtend at the center. We know that the sum of all angles subtended at the center of the circle is $360{}^\circ $.
So we have $\alpha +\beta +\gamma =360{}^\circ $
Now, the arithmetic mean will be given as
$\Rightarrow \dfrac{\cos \left( \alpha +\dfrac{\pi }{2} \right)+\cos \left( \beta +\dfrac{\pi }{2} \right)+\cos \left( \gamma +\dfrac{\pi }{2} \right)}{3}$
Now, we have to find the minimum value and the arithmetic mean has minimum value when
\[\begin{align}
  & \Rightarrow \cos \left( \alpha +\dfrac{\pi }{2} \right)=\cos \left( \beta +\dfrac{\pi }{2} \right)=\cos \left( \gamma +\dfrac{\pi }{2} \right) \\
 & \Rightarrow \left( \alpha +\dfrac{\pi }{2} \right)=\left( \beta +\dfrac{\pi }{2} \right)=\left( \gamma +\dfrac{\pi }{2} \right) \\
 & \Rightarrow \alpha =\beta =\gamma \\
 & \Rightarrow \alpha =\beta =\gamma =120{}^\circ \\
\end{align}\]
Now, substituting the value in the above obtained equation we will get
\[\begin{align}
  & \Rightarrow \dfrac{3\cos \left( 120{}^\circ +\dfrac{\pi }{2} \right)}{3} \\
 & \Rightarrow \dfrac{3\cos \left( 210{}^\circ \right)}{3} \\
 & \Rightarrow \cos \left( 210{}^\circ \right) \\
 & \Rightarrow -\dfrac{\sqrt{3}}{2} \\
\end{align}\]
Hence we get that minimum value of the arithmetic means of $\cos \left( \alpha +\dfrac{\pi }{2} \right),\cos \left( \beta +\dfrac{\pi }{2} \right)$ and $\cos \left( \gamma +\dfrac{\pi }{2} \right)$ is equal to \[-\dfrac{\sqrt{3}}{2}\].

So, the correct answer is “Option D”.

Note: The point to be noted is that the value of arithmetic mean is always greater than or equal to the value of geometrical mean for the same data. We used this concept to find the minimum value of the arithmetic means of the given data.