Question

The sides of an equilateral triangle are \[\left( 3x+2y \right)\] cm, \[\left( 5x+6y \right)\] cm, and \[\left( x+y+3 \right)\] cm. Then the perimeter of the triangle is
A.15 cm
B.12 cm
C.18 cm
D.10.5 cm

Answer 1

Hint: We know that an equilateral triangle has all sides equal to each other. Here, we have the lengths of sides as \[\left( 3x+2y \right)\] cm, \[\left( 5x+6y \right)\] cm, and \[\left( x+y+3 \right)\] cm. So, each side will be equal to each other. Now, solve for x and y. We know that the perimeter of a triangle is the sum of its all sides. Now, solve it further.

Complete step-by-step answer:
According to the question, we have an equilateral triangle whose sides are \[\left( 3x+2y \right)\] cm, \[\left( 5x+6y \right)\] cm, and \[\left( x+y+3 \right)\] cm.

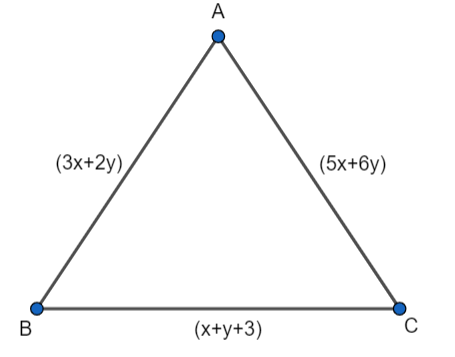
We know the property of an equilateral triangle that all sides of an equilateral triangle are equal to each other.
So, using this property we can say that the sides \[\left( 3x+2y \right)\] cm, \[\left( 5x+6y \right)\] cm, and \[\left( x+y+3 \right)\] cm are equal to each other.
\[\left( 3x+2y \right)=\left( 5x+6y \right)\] ……………………..(1)
\[\left( 5x+6y \right)\text{ = }\left( x+y+3 \right)\] ……………………(2)
Now, solving equation (1), we get
\[\begin{align}
  & \left( 3x+2y \right)=\left( 5x+6y \right) \\
 & \Rightarrow 3x-5x=6y-2y \\
 & \Rightarrow -2x=4y \\
\end{align}\]
\[\Rightarrow x=-2y\] …………………..(3)
Now, solving equation (2), we get
\[\begin{align}
  & \left( 5x+6y \right)\text{ = }\left( x+y+3 \right) \\
 & \Rightarrow 5x-x+6y-y=3 \\
\end{align}\]
\[\Rightarrow 4x+5y=3\] …………………..(4)
Substituting the value of x from equation (3), in the equation (4), we get
\[\begin{align}
  & \Rightarrow 4x+5y=3 \\
 & \Rightarrow -8y+5y=3 \\
 & \Rightarrow -3y=3 \\
 & \Rightarrow y=-1 \\
\end{align}\]
Putting y=-1 in equation (3), we get
\[\begin{align}
  & \Rightarrow x=-2(-1) \\
 & \Rightarrow x=2 \\
\end{align}\]
The length of one side is \[\left( 3x+2y \right)=3\left( 2 \right)+2\left( -1 \right)=6-2=4\] .
All three sides are equal to each other. The length of one side is 4cm. So, the length of each side is 4 cm.
We know that the perimeter of a triangle is the sum of its all sides.
So, Perimeter = (4 + 4 + 4)cm = 12cm.
Hence, the correct option is (B).

Note: In this question, one may miss the negative sign in -1 that is one can take y as 1 and x as 2. Then, the length of each side will be \[\left( 3x+2y \right)\] which is equal to 8. Our perimeter will be 24. This is completely wrong. So, we have to be attentive towards the calculation and the negative sign should be kept in mind.