Question

The slope of velocity (v) vs. time (t) curve at any instant of time gives:
A. displacement
B. velocity
C. acceleration
D. all of the above

Answer 1

Hint: Velocity can be defined as the rate of change of position with time. The slope of a distance or position-time graph at any time is velocity and acceleration is the rate of change of velocity. Simply use the formula which will give the relation between velocity and time.

Complete step by step answer:

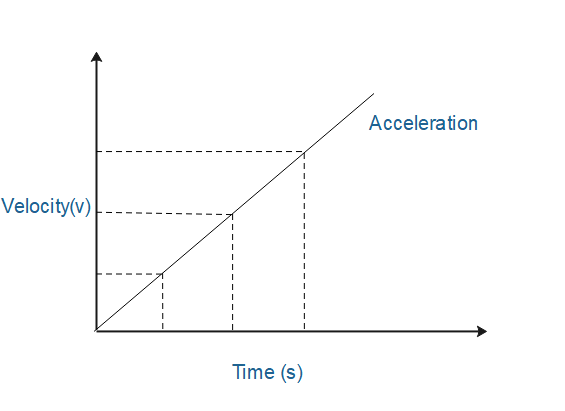
Expression of the slope is given by,
Slope=$\dfrac{y}{x}$
Slope of v-s graph is equal to $\dfrac{dv}{dt}=a$
As you can in the graph, the shape of a velocity versus time graph reveals pertinent information about an object's acceleration. For example, if the acceleration is zero, then the velocity-time graph is a horizontal line that is the slope is zero). If the acceleration is positive, then the line is an upward sloping line (that is the slope is positive). If the acceleration is negative, then the velocity-time graph is a downward sloping line (that is the slope is negative). If the acceleration is great, then the line slopes up steeply (that is the slope is great).
This principle can be extended to any type of motion conceivable. Thus the shape of the line on the graph is descriptive of the object's motion.
Hence, the slope of velocity (v) vs. time (t) curve at any instant of time gives acceleration. Therefore the correct option is (C).

Note:
The actual slope value of any straight line on a velocity-time graph is the acceleration of the object. A student of physics must have a good understanding of how to calculate the slope of a line. The slope equation implies that the slope of a line is found by determining the amount of rising of the line between any two points divided by the amount of run of the line between any, same two points.