Question

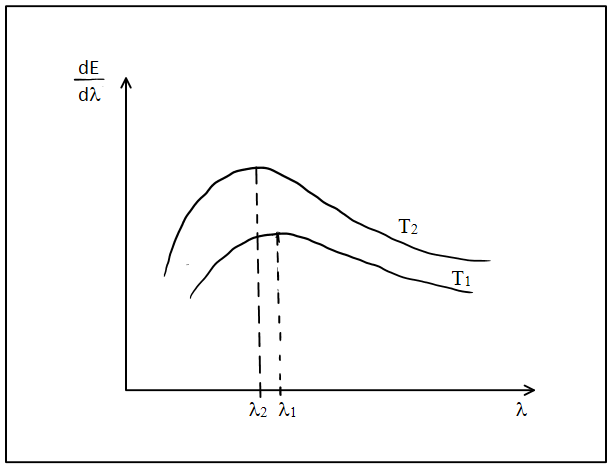
The spectral emissive power ${E_\lambda }$ for a body at temperature T₁ is plotted against the wavelength and area under the curve is found to be A. At a different temperature T₂ the area is found to be 9A. Then $\dfrac{{{\lambda _1}}}{{{\lambda _2}}}$ is

(A) 3
(B) $\dfrac{1}{3}$
(C) $\dfrac{1}{{\sqrt 3 }}$
(D) $\sqrt 3 $

Answer 1

Hint: The area under enclosed by the graph formed between the quantities ${E_\lambda }$and $\lambda $ denotes the total emissive power radiated by the body. And total emissive power radiated by a body can be calculated by stefan’s law, $E = e\sigma {T^4}$, where E denotes total emissive power, e denotes emissivity of the body, σ is the stefan’s constant and T denotes absolute temperature of the body. The wavelength at which spectral emissive power is maximum relates to the temperature according to wein’s displacement law i.e. ${\lambda _1}{T_1} = {\lambda _2}{T_2}$ .

Complete step by step solution:
The total area under the graph formed between the quantities ${E_\lambda }$ and $\lambda $ denotes total emissive power radiated by a body.
Given that total emissive power at temperature T₁ is A,

Using Stefan's law we can say that : $A = e\sigma {T_1}^4$ .
Given that total emissive power at temperature T₂ is 9A,

Using Stefan's law we can say that $9A = \sigma {T_2}^4$.
Dividing these two equations, we get :
\[\dfrac{A}{{9A}} = \dfrac{{\sigma {T_1}^4}}{{\sigma {T_2}^4}}\] ,
Cancelling A and σ on both sides, we get :
 \[\dfrac{1}{9} = \dfrac{{{T_1}^4}}{{{T_2}^4}}\],
Cross multiplication gives,
\[{T_2}^4 = 9{T_1}^4\],
Raising power $\dfrac{1}{4}$ on both sides, we get :
\[{T_2}^{} = {T_1}^{}\sqrt 3 \]
Now, using wien's displacement law :
${\lambda _1}{T_1} = {\lambda _2}{T_2}$,
Substituting the value of T₂, we get :
${\lambda _1}{T_1} = {\lambda _2}{T_1}\sqrt 3 $,
Cancelling T₁ on both sides :
${\lambda _1} = {\lambda _2}\sqrt 3 $,
$\dfrac{{{\lambda _1}}}{{{\lambda _2}}} = \sqrt 3 $

Therefore the correct answer is option : (D)

Note: Before solving the problem, the student needs to be able to understand the different concepts of Radiation like Stefan’s law, Wien's Displacement law and the terms like total emissive power and spectral emissive power. A common mistake that students make while solving questions involving concepts of radiation is not being able to differentiate between spectral emissive power and total emissive power. While total emissive power is the intensity of radiation emitted by a body, spectral emissive power is the intensity of radiation emitted by a body per unit wavelength.