Question

The statue of height 1.46 metres is placed on a table of certain height. The angle of elevation of the top of the statue from the point on the ground is ${60^ \circ }$ and that of the top of the table is ${45^ \circ }$. Find the height of the table.

Answer 1

Hint: First try to draw a figure from the given data and from that using trigonometric ratios try to find out the required data (that is the height of the table).

Complete step-by-step answer:
From the given data, let us construct a rough figure:

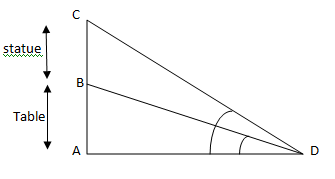
Given that the height of the statue=1.46 metres
Also, given that the angle of elevation of the top of the statue from a point on the ground
=$\angle ADB = {60^0}$
Angle of elevation of the top of the table from a point on the ground
=$\angle ADC = {45^0}$
Let h be the height of the table,
In the question we have been asked to find out the height of table that is AB
So, to find out this let us make use of the trigonometric ratio tan and try to solve it
In triangle ABD, we can write
$\tan {45^0} = \dfrac{{AB}}{{AD}}$
$
   \Rightarrow 1 = \dfrac{{AB}}{{AD}} \\
   \Rightarrow 1 = \dfrac{h}{x} \\
$
From this, we get h=x--------(i)
Similarly in triangle ABC, we can write
$
 \tan {60^ \circ } = \dfrac{{AC}}{{AD}} \\
  \tan {60^ \circ } = \dfrac{{h + 1.46}}{x} \\
    \\
$
Let’s substitute the value of $\tan {60^ \circ }$ in the above equation,
So we get $\sqrt 3 = \dfrac{{h + 1.46}}{x}$ ------(ii)
From eq (i) , let us substitute h=x in this equation,
So, we get
$
  \sqrt 3 = \dfrac{{h + 1.46}}{h} \\
   \Rightarrow \sqrt 3 - 1 = \dfrac{{1.46}}{h} \\
$
So, on solving this further we get that the height of the table=h=1.994metres
So, the height of the table = 1.994metres.
Note: When solving these type of problems make use of the appropriate trigonometric ratios which will actually help us in finding out the required value