Question

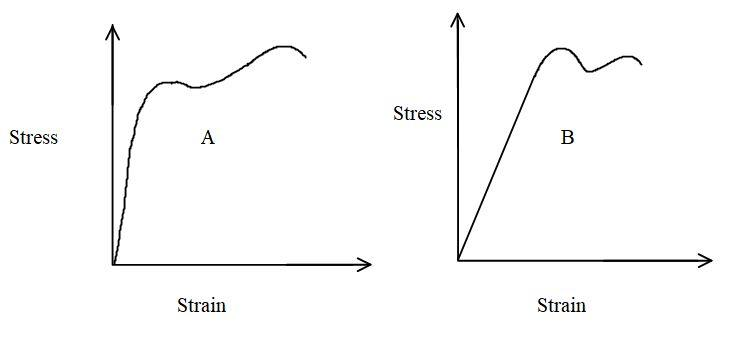
The stress-strain graphs for materials A and B are shown in figure. The graphs are drawn to the same scale.
a) Which of the materials has the greater Young’s modulus?
b) Which of the two is the stronger material?

Answer 1

Hint: The slope of stress-strain diagram gives the Young’s modulus of a material. Young’s modulus tells us about the strength of the material. The elastic region or the linear region in the graph is the point until which Hooke’s law is applicable which relates stress and strain to the Young’s Modulus of the material.

Complete step by step answer:
The slope of any stress-strain graph gives us the Young’s modulus, so we can compare the slope of the two graphs and we can know about the Young’s modulus of the different materials.
After observing the two graphs we can conclude that the slope for material A is more than the slope for material B, which means that the Young’s modulus of material A is more than the Young’s modulus of material B.
So, the answer for the first part of the problem is, the material A has more Young’s modulus as compared to Young’s modulus of body B.
Now, let us get into which material is stronger among material A and B.
Young’s modulus gives the measure of strength of any material and we already know from the first part of the problem that the Young’s modulus of material A is more than Young’s modulus of material B this means that material A is more stronger than material B. So, the answer for second problem is that the material A is stronger than material B.

Additional Information: The Young’s Modulus of a material signifies it’s stiffness or it’s resistance to plastic deformation. Higher is the Young’s Modulus, stiffer is the material.

Note: Stress strain diagrams of a material are important for any material and many properties of material are known by the relationship between stress and strain. A relationship between stress and strain is given as $\sigma = {\text{E}} \cdot \varepsilon $. Where stress is $\sigma $, Young’s modulus is ${\text{E}}$ and strain is $\varepsilon $ of the material.