Question

The sum of the exterior angles of a hexagon is:
A.$360^\circ $
B.$540^\circ $
C.$720^\circ $
D.None of these

Answer 1

Hint: We can draw a hexagon and mark its interior angles and exterior angles. An interior angle exterior angle pair will be supplementary. So, we can take the sum of all the exterior and interior angles. From that we can subtract the sum of interior angles to get the sum of exterior angles. The sum of interior angles can be calculated using the equation $\left( {n - 2} \right)180^\circ $.

Complete step-by-step answer:
We know that hexagon is a polynomial with 6 sides and angles. We can draw a hexagon and mark its interior and exterior angles.

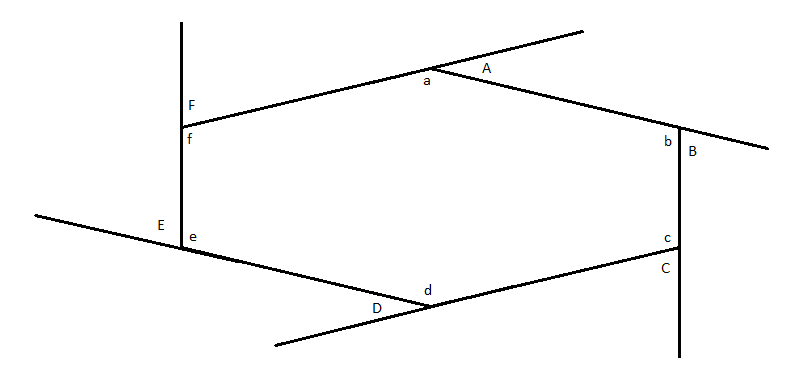
In the figure, $\angle a,\angle b....\angle f$are the interior angle and $\angle A,\angle B....\angle F$are the corresponding exterior angles. We know that exterior angles are angles that are formed at the vertices when one side is extended outside the polynomial. So, the sum of an interior angle and its corresponding exterior angle will be $180^\circ $as they form a linear pair.
\[ \Rightarrow \angle a + \angle A = 180^\circ ,\angle b + \angle B = 180^\circ ,.....,\angle f + \angle F = 180^\circ \]
As a hexagon has 6 angles, it will have 6 interior angle exterior angle pair. Adding all the equations above, we get,
\[ \Rightarrow \angle a + \angle A + \angle b + \angle B + ..... + \angle f + \angle F = 180^\circ \times 6\]
We can write the exterior angles and interior angles separately.
\[ \Rightarrow \left( {\angle a + \angle b + .. + \angle f} \right) + \left( {\angle A + \angle B + .. + \angle F} \right) = 1080^\circ \]… (1)
We know that the sum of the interior angles of a polygon is given by the equation $\left( {n - 2} \right) \times 180^\circ $. As a hexagon has 6 sides, sum of the angles is given by
$\left( {6 - 2} \right) \times 180^\circ = 4 \times 180^\circ = 720^\circ $
Therefore, we can write the sum in terms of the angles of our hexagon,
\[ \Rightarrow \left( {\angle a + \angle b + .. + \angle f} \right) = 720^\circ \] …. (2)
Subtracting (2) from (1), we get,
\[
  \left( {\angle a + \angle b + .. + \angle f} \right) + \left( {\angle A + \angle B + .. + \angle F} \right) - \left( {\angle a + \angle b + .. + \angle f} \right) = 1080^\circ - 720^\circ \\
   \Rightarrow \left( {\angle A + \angle B + .. + \angle F} \right) = 360^\circ \\
 \]
Now we have the sum of the exterior angles as $360^\circ $
Therefore, the correct answer is option A.

Note: When a side of a polygon is extended at a vertex, it forms an angle with the adjacent side outside the polygon. This angle of a polygon is known as exterior angle. As the exterior angle and interior angle forms a linear pair, they will be supplementary or their sum will be equal to$180^\circ $. We are using this concept to solve this problem. As the interior and exterior angle pairs will be supplementary for any polygon with any number of sides, this method can be used to find the sum of exterior angles of any polygon. We can form two exterior angles at a vertex and they both will be equal. We must consider only one exterior angle per vertex. For a regular polygon, all the exterior angles will be equal as their internal angles are equal.