Question

The sum of the lengths of all the edges of a cube is 6cm. What is the volume of the cube, in cubic centimeters?

Answer 1

Hint – In this question the length of all the edges are given so the length of a single edge can be taken out by assuming the length of one edge to be a variable x. Use the direct formula for volume of a cube which is $V = {x^3}{\text{ c}}{{\text{m}}^3}$.

Complete step-by-step answer:

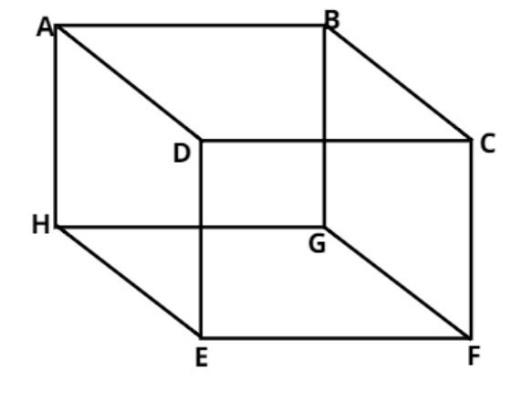
The cube ABCDEFGH is shown above.
As we know that in a cube all the sides are equal.
And there are 12 edges in a cube whose names is written below
$\left( i \right)$ AB, $\left( {ii} \right)$ AD, $\left( {iii} \right)$ DC, $\left( {iv} \right)$CB, $\left( v \right)$ CF, $\left( {vi} \right)$ BG, $\left( {vii} \right)$ DE, $\left( {viii} \right)$ AH, $\left( {ix} \right)$ EH, $\left( x \right)$ EF, $\left( {xi} \right)$ FG and$\left( {xii} \right)$ GH.
Let the length of one edge is x cm.
Now it is given that the sum of the lengths of all the edges of a cube is 6 cm.
$ \Rightarrow 12x = 6{\text{ cm}}$
Therefore length of one edge is
$ \Rightarrow x = \dfrac{6}{{12}} = \dfrac{1}{2}{\text{ cm}}$
Now as we know that the volume (V) of the cube is side cube.
$ \Rightarrow V = {x^3}{\text{ c}}{{\text{m}}^3}$
Now substitute the value of x we have,
$ \Rightarrow V = {\left( {\dfrac{1}{2}} \right)^3} = \dfrac{1}{8}{\text{ c}}{{\text{m}}^3}$
So this is the required volume of the cube.
So this is the required answer.

Note – A cube is a symmetrical three-dimensional shape, which is either solid or hollow, and is contained by six equal squares. The given length of all the edges depicts the perimeter as in mathematics it is defined as the sum of all sides.