Question

The sum of the slopes of the lines tangent to both the circles \[{x^2} + {y^2} = 1\] and \[{\left( {x - 6} \right)^2} + {y^2} = 4\] is _____.

Answer 1

Hint: To find the slope of the line joining two points \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\] then we will use the formula \[m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\] and if the equation of the line is given as \[y = mx + c\] then the slope of this line will be m.

Complete step-by-step answer:
As we know that the standard equation of the circle is ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$. And the centre of this circle is (a, b) and its radius is r.
So, comparing equations of both of the circles to get their radius and centre.
So, the centre of the circle \[{x^2} + {y^2} = 1\] will be (0, 0) and radius = 1 units.
And the centre of the circle \[{\left( {x - 6} \right)^2} + {y^2} = 4\] will be (6, 0) and radius = 2 units.
Now let us plot both the circles in the coordinate plane.

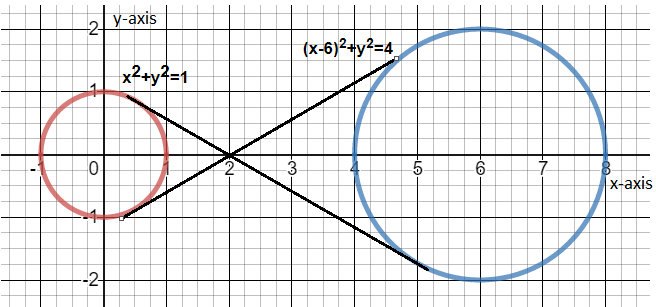
Now we can see from the above figure that both the circles are symmetric around the x-axis.
So, the angle made by the common tangents to both of the circles will be equal and opposite.
And as we know that the tan of the angle made any line with x axis is the slope of the line.
So, the slopes of the common tangents to both the circles will be equal and opposite.
Hence, the sum of the slopes of the tangents to the circle \[{x^2} + {y^2} = 1\] and \[{\left( {x - 6} \right)^2} + {y^2} = 4\] will be equal to 0.

Note: Whenever we come up with this type of problem we should first, first find the centre and the radius of the given circles by comparing their equation with the standard equation of circle that is ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {r^2}$ and whose centre and radius are (a, b) and r units. After that we had to plot the circles in the cartesian plane. So, that we can see the symmetry of the circles. And after that we should remember that the slope of a line is the tangent of its angle made with a positive direction of x-axis. And if two circles are symmetric about the x-axis then the sum of slopes of their tangents must be equal to zero because their common tangents have equal and opposite slopes. So, this will be the easiest and efficient way to find the solution of the problem.