Question

The sum of two negative integers is always a _____ integer.

Answer 1

Hint: Here, we will use the concept of an integer. Then we will show how two positive integers are added. Using the same concept, we will show the addition of negative integers. Then we will also show the addition of negative integers using the number line.

Complete step by step solution:
An integer is a number which can be negative, positive or 0. This sign can either be positive \[( + )\] or negative \[( - )\]. As such, the integer \[0\] is neither positive nor negative. Also, we need not denote positive integers with the \[( + )\] sign. But the negative integers must be denoted by a \[( - )\] sign. For example, \[ - 5\] is a negative integer.
Let us now demonstrate how positive integers and negative integers are added.
To add positive integers is just like usual addition. When we add two or more positive integers, we get the result as a positive integer.
Example: \[13 + 7 = 21\]
The same applies to negative integer addition. When we add two negative integers, the result is a negative integer. To add two or more negative integers, ignore the \[( - )\] sign and add the integers like usual addition. Then, to the result, attach the \[( - )\] sign.
Example: \[( - 13) + ( - 7) = ( - 21)\]
Now, on the number line, the positive integers lie on the right of zero and the negative integers lie on the left of zero. The integer line is represented as follows:

To add integers using the integer line, we have to begin at the first number and count the number of steps as the second number. If the integers are positive, we move towards the right. If the integers are negative, we move towards the left.
Suppose we want to add \[ - 1\] and \[ - 2\]. To do this, we start at \[ - 1\] and go \[2\] steps to the right.

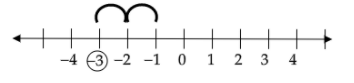
We observe that we reach at \[ - 3\]. Thus, \[( - 1) + ( - 2) = ( - 3)\]

Therefore, the sum of two negative integers is always a negative integer.

Note:
To add two or more integers of the same sign is simply like usual addition and the final result must have the same sign as the addends. But if we want to add a positive integer to a negative integer, the sign plays an important role. In this case, we have to subtract the two integers, and the result must have the sign of the integer which has a bigger value (ignoring the sign). For example, to add \[ - 13\] and \[7\], we have to ignore the signs and subtract. The result is 6. Since 13 is bigger than 7, we will put the sign of 13 to 6. So, \[( - 13) + 7 = ( - 6)\].