Question

The surface of a polar liquid such as water, can be viewed as a series of dipole strung together in the stable arrangement in which dipole moment vectors are parallel to the surface and all point in the same direction. Now suppose that something is pressing downwards (inwards) on the surface distorting the dipoles as shown in figure.
Then the slanted dipoles will exert a net force in which direction

(A) Downward
(B) Upward
(C) Horizontal
(D) None of these

Answer 1

Hint: In a field of charge, the unlike charges tend to move towards each other while the like charges move away from each other. The resultant of the force on the centre non-slanted charge due to the neighbouring slanted dipoles determines the direction of the net force.

Complete step by step solution:

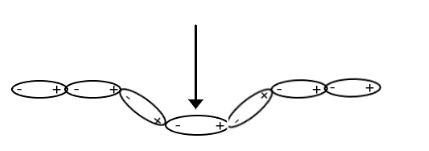
The neighbouring charges of the string of dipoles tend to attract each other i.e. the positive charge at the end of one dipole attracts the negative charge at the end of the next dipole, which prevent any tendency for the opposite charge within a dipole to depolarize, i.e. recombine to give a dipole of zero. The direction of these forces are in such a way that they are parallel to the dipole or charge creating the force.
Now, as one of the dipoles is pressed downward, the attraction between its charges and the neighbouring dipole charge allows the neighbouring dipole to slant as shown in the figure.
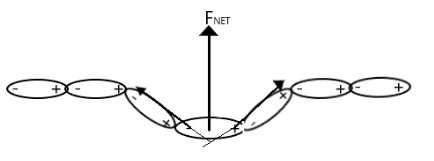
However, according to Newton’s third law, action and reaction are equal and opposite. Thus as the pressed dipole attracted the slanted neighbouring dipoles to itself, the slanted neighbouring dipoles also exert a force on the pressed dipole towards themselves in the direction parallel to the slanted dipoles as shown.
Since there are molecules of the same element, the force exerted by the left slanted dipole is equal to the force exerted by the right slanted dipole, hence, in the horizontal direction, these forces cancel out each other, and however, as seen the forces both attract the mid dipole in an upward direction which is not balance by any internal force.
Thus, the net force is in the upward direction.
So the correct option is B.

Note:
Alternatively we can also solve this problem as, in mathematical terms, the force exerted by the charges of the slanted dipoles on the mid dipole is given as
 $\Rightarrow F = k\dfrac{{{q^2}}}{{{r^2}}} $ where $ q $ is the charge of the each of the two charges, $ r $ is the distance between them, and $ k $ is a constant.
Now, the horizontal component of the force exerted by right slanted dipole is
 $\Rightarrow F = k\dfrac{{{q^2}}}{{{r^2}}}\cos \theta $ where $ \theta $ is the angle between the force and the horizontal
While the vertical component is
 $\Rightarrow F = k\dfrac{{{q^2}}}{{{r^2}}}\sin \theta $
The horizontal force exerted by the left slanted dipole is
 $\Rightarrow F = - k\dfrac{{{q^2}}}{{{r^2}}}\cos \theta $ (assume leftward is negative)
And the vertical component
 $\Rightarrow F = k\dfrac{{{q^2}}}{{{r^2}}}\sin \theta $
Summing up the horizontal components of the two forces we have that
 $\Rightarrow {F_H} = k\dfrac{{{q^2}}}{{{r^2}}}\cos \theta + \left( { - k\dfrac{{{q^2}}}{{{r^2}}}\cos \theta } \right) = 0 $
For vertical component
 $\Rightarrow {F_H} = k\dfrac{{{q^2}}}{{{r^2}}}\sin \theta + k\dfrac{{{q^2}}}{{{r^2}}}\sin \theta = 2k\dfrac{{{q^2}}}{{{r^2}}}\sin \theta $
Hence net force is in vertical direction.