Question

The surface tension of a soap solution is $25\times {{10}^{-3}}N{{m}^{-1}}$. The excess pressure inside a soap bubble of diameter $1cm$ is
$\begin{align}
  & \text{A}\text{. }5Pa\text{ } \\
 & \text{B}\text{. }10Pa\text{ } \\
 & \text{C}\text{. }20Pa\text{ } \\
 & \text{D}\text{. }40Pa\text{ } \\
\end{align}$

Answer 1

Hint: Surface tension is a property of the liquid surface acting as if it were a stretched elastic membrane. The inward net force results in more pressure inside than outside and causes the liquid molecules on the surface to contract and to resist being stretched or broken.

Complete step by step answer:
Consider a soap bubble having radius R and surface tension T. There are two free surfaces in a soap bubble. Due to the surface tension, the molecules present on the surface film experience a net force in the inward direction normal to the surface. Thus, there is more pressure inside than outside.

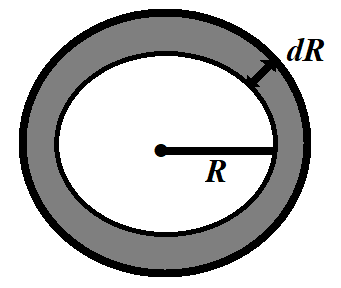
Let ${{p}_{i}}$ be the pressure inside the soap bubble and ${{p}_{o}}$ be the pressure outside the soap bubble. Therefore, excess pressure inside the soap bubble is given by:
$p={{p}_{i}}-{{p}_{o}}$
Due to excess pressure inside the soap bubble, the free surface of the bubble will experience a net force in the outward direction due to which the bubble will expand.
Let the free surfaces be displaced by $dR$ under isothermal conditions. Therefore, the excess pressure does the work in displacing the surface and that work will be stored in the form of potential energy inside the soap bubble.
The work done by excess pressure in displacing the surface is
$dW=\text{ force }\times \text{ displacement}$
That is,
$dW=\text{excess pressure }\times \text{ Surface area }\times \text{ displacement of surface}$
Putting values,
$dW=p\times 4\pi {{R}^{2}}\times dR$
(Let’s say equation 1)
Increase in the potential energy of the bubble,
$dU=\text{Surface tension }\times \text{ increase in area of the free surface}$
Or,
$\begin{align}
  & dU=T\left[ 2\left\{ 4\pi {{\left( R+dR \right)}^{2}}-4\pi {{R}^{2}} \right\} \right] \\
 & dU=T\left[ 2\left\{ 4\pi \left( 2R\times dR \right) \right\} \right] \\
\end{align}$
(Let’s say equation 2)
From equation 1 and equation 2,
$p\times 4\pi {{R}^{2}}\times dR=T\left[ 2\left\{ 4\pi \left( 2RdR \right) \right\} \right]$
Therefore,
$p=\dfrac{4T}{R}$
We are given that the surface tension of a soap solution is $25\times {{10}^{-3}}N{{m}^{-1}}$ and the diameter of the soap bubble is $1cm$. We have to calculate the excess pressure inside the soap bubble.
Given,
Diameter of soap bubble $d=1cm$
Therefore,
Radius $R=\dfrac{1}{200}m$
Now,
Excess pressure inside soap bubble is given as,
$p=\dfrac{4T}{R}$
Where,
$T$ is the surface tension
$R$ is the radius of the soap bubble
Putting values,
$\begin{align}
  & T=25\times {{10}^{-3}}N \\
 & R=\dfrac{1}{200}m \\
\end{align}$
We get,
$\begin{align}
  & p=\dfrac{4\times 25\times {{10}^{-3}}}{\dfrac{1}{200}}=4\times 25\times 200\times {{10}^{-3}} \\
 & p=20N{{m}^{-2}} \\
\end{align}$
As we know,
$1Pa=1N{{m}^{-2}}$
Therefore,
$p=20Pa$
The excess pressure inside the soap bubble is $20Pa$
Hence, the correct option is C.

Note:
The soap bubble has two air-liquid interfaces. The soap bubble is a thin layer of liquid. It has some finite thickness. The outside of the soap is in touch with the air outside the bubble, which is considered as the first surface and the inside of the soap is touching the air inside the bubble, which is the second surface.