Question

The surface tension of water is determined by capillary rise method in the laboratory. The principle involved is (symbols having their usual meaning):
A. $T=\dfrac{r}{3}\left(h+\dfrac{r}{3}\right)dg$
B.$T=\dfrac{r}{4}\left(h+\dfrac{r}{2}\right)dg$
C.$T=\dfrac{r}{2}\left(h+\dfrac{r}{3}\right)dg$
D.$T=\dfrac{r}{2}\left(\dfrac{h}{3}+r\right)dg$

Answer 1

Hint: We know that surface tension is the tendency of liquids to shrink or reduce the surface area of the liquid at the liquid air interface, due to the difference in the force of attraction of cohesion between the different interfaces present. And this is measured in SI units

Complete step-by-step solution:
To find or calculate the surface tension of liquids, we use the capillary rise method, where a thin tube called the capillary is introduced into the liquid, whose surface tension is to be studied.
This results in the rise of liquid inside the constrained spaces of the tube. The length of rise is proportional to the surface tension of the liquid.

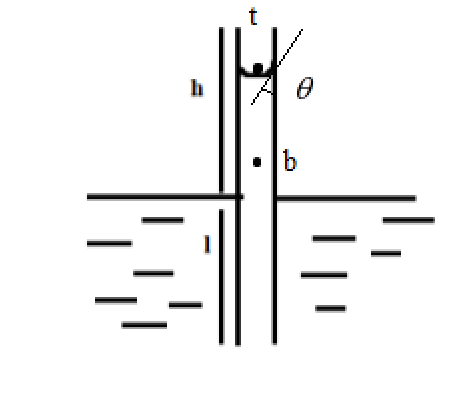
From Jurin’s law, we have, just above the liquid-air interface, the pressure experienced by the water molecules is equal to the atmospheric pressure.
$p_t=p_o+ p$
At any point inside the liquid, the pressure experienced by the liquid is less than the sum of the pressure due to the liquid and the pressure due to the atmosphere.
$p_b=p+p_l$
The pressure due to liquid depends on the height of liquid column $h$ above the point of interest and the density of the liquid $d$
$p_l=dgh$
Since there is an angle made at the liquid air interface, we have
$dgh=\dfrac{2\gamma cos \theta}{r}$ where, $\gamma$ is the surface tension due to contact angle $\theta$ and $r$ is the radius of the capillary tube.
Then, at any point in liquid, we have
$\gamma=\dfrac{r}{2cos\theta}dgh$
$\implies \gamma=\dfrac{r}{2}\left(\dfrac{h}{3}+r\right)dg$
Hence the answer is D. $T=\dfrac{r}{2}\left(\dfrac{h}{3}+r\right)dg$

Note: This is observed as the combined effect of the cohesive force acting between the liquid-liquid interface and the liquid –capillary. The difference between the attraction, results in the formation of meniscus, which tries to minimize the distance between the water molecules by attracting or pulling them closer to one another.