Question

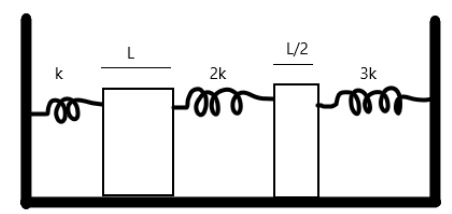
The system shown in figure consists of three springs and two rods as shown. If the temperature of the rods is increased by $ \Delta T $ , calculate the energy stored in each of the springs. The springs are initially relaxed. There is no friction. Take the coefficient of linear expansion of the material of rods to be equal to $ \alpha $ -

Answer 1

Hint : The extension of the length of the rod will cause an extension in the string. The rod will extend equally in both left and right directions. Observe that the middle spring will be doubly compressed due to the extension of the two rods.

Formula used: In this solution we will be using the following formulae;
 $ E = \dfrac{1}{2}k{e^2} $ where $ E $ is the energy stored in a spring, $ k $ is the spring constant of the spring and $ e $ is the extension or compression of the spring from equilibrium position.
 $ \alpha = \dfrac{{\Delta L}}{{L\Delta T}} $ where $ \alpha $ is the coefficient of linear expansion of a material, $ \Delta L $ is the increase in length of the body, $ L $ is the initial length and $ \Delta T $ is the change in temperature of the substance.

Complete step by step answer
To calculate the energy stored in each of the springs, we note that the extension in length due to the change in temperature of the substance causes the springs to compress. Hence, we must calculate the extensions. The coefficient of linear expansion can be given by
 $ \alpha = \dfrac{{\Delta L}}{{L\Delta T}} $ where $ \Delta L $ is the increase in length of the body, $ L $ is the initial length and $ \Delta T $ is the change in temperature of the substance.
So for the rod of length $ L $ , we have a change in length of
 $ \Delta {L_1} = \alpha L\Delta T $
And hence similarly for the rod of length $ \dfrac{L}{2} $
 $ \Delta {L_2} = \alpha \dfrac{L}{2}\Delta T $
Now, the length increases equally in both directions. Hence the compression in the first spring is $ \dfrac{{\Delta {L_1}}}{2} $
The energy in a spring can be given by $ E = \dfrac{1}{2}k{e^2} $ where $ k $ is the spring constant of the spring and $ e $ is the extension or compression of the spring from equilibrium position.
Hence, the energy of first spring is
 $ E = \dfrac{1}{2}k{\left( {\dfrac{{\Delta L}}{2}} \right)^2} $
Then, by inserting the expression for $ \Delta L $ , we have
 $ E = \dfrac{1}{2}k{\left( {\dfrac{{\alpha L\Delta T}}{2}} \right)^2} = \dfrac{1}{8}k{\alpha ^2}{L^2}\Delta {T^2} $
For the second spring, it is compressed by $ \dfrac{{\Delta {L_1}}}{2} $ from the left, and by $ \dfrac{{\Delta {L_2}}}{2} $ from the right, hence the total extension is $ \dfrac{{\Delta {L_1}}}{2} + \dfrac{{\Delta {L_2}}}{2} $
Then,
 $ {E_2} = \dfrac{1}{2}2k{\left( {\dfrac{{\Delta {L_1}}}{2} + \dfrac{{\Delta {L_2}}}{2}} \right)^2} $
Inserting known expressions, we get
 $ {E_2} = \dfrac{1}{2}2k{\left( {\dfrac{{\alpha L\Delta T}}{2} + \dfrac{{\alpha \dfrac{L}{2}\Delta T}}{2}} \right)^2} = \dfrac{1}{2}2k{\left( {\dfrac{{3\alpha L\Delta T}}{4}} \right)^2} $
By simplification
 $ {E_2} = \dfrac{9}{{16}}k{\alpha ^2}{L^2}\Delta {T^2} $
For the third spring, the extension is $ \dfrac{{\Delta {L_2}}}{2} $
Hence,
 $ {E_3} = \dfrac{1}{2}3k{\left( {\dfrac{{\alpha \dfrac{L}{2}\Delta T}}{2}} \right)^2} $
Hence, by simplification, we have
 $ {E_3} = \dfrac{1}{2}3k{\left( {\dfrac{{\alpha L\Delta T}}{4}} \right)^2} $
 $ \Rightarrow {E_3} = \dfrac{1}{2}3k{\left( {\dfrac{{\alpha L\Delta T}}{4}} \right)^2} = \dfrac{3}{{32}}k{\alpha ^2}{L^2}\Delta {T^2} $ .

Note
For clarity, note that the substance is assumed to have increased equally in both directions. This happens when the temperature is evenly distributed along the line parallel to the length. In such a case where it isn’t the assumption in invalid.