The tangent and normal at the point $P\left( a{{t}^{2}},2at \right)$ to the parabola ${{y}^{2}}=4ax$ meet the x-axis in T and G respectively, then the angle at which the tangent at P to the parabola is inclined to the tangent at P to the circle through P, T, G is
(a) ${{\tan }^{-1}}\left( {{t}^{2}} \right)$.
(b) ${{\cot }^{-1}}\left( {{t}^{2}} \right)$.
(c) ${{\tan }^{-1}}\left( t \right)$.
(d) ${{\cot }^{-1}}\left( t \right)$.
Answer
Verified475.8k+ views
Hint: We find the slope and equation of the tangent through which we find the point T. We use the fact that normal is perpendicular to tangent to find the equation of the normal. Once we find the equation of the normal, we calculate the point G. After finding all these points we calculate the equation of the circle and subsequently the equation of tangent. Using the slope of tangents we find the angle between them.
Complete step by step answer:
Given that we have a parabola ${{y}^{2}}=4ax$, the tangent and normal at the point $P\left( a{{t}^{2}},2at \right)$ to the parabola meets x-axis at the points T and G. We need to find the angle between tangent at P for parabola and tangent at P to the circle passing through P, T, G.
Let us draw the given information
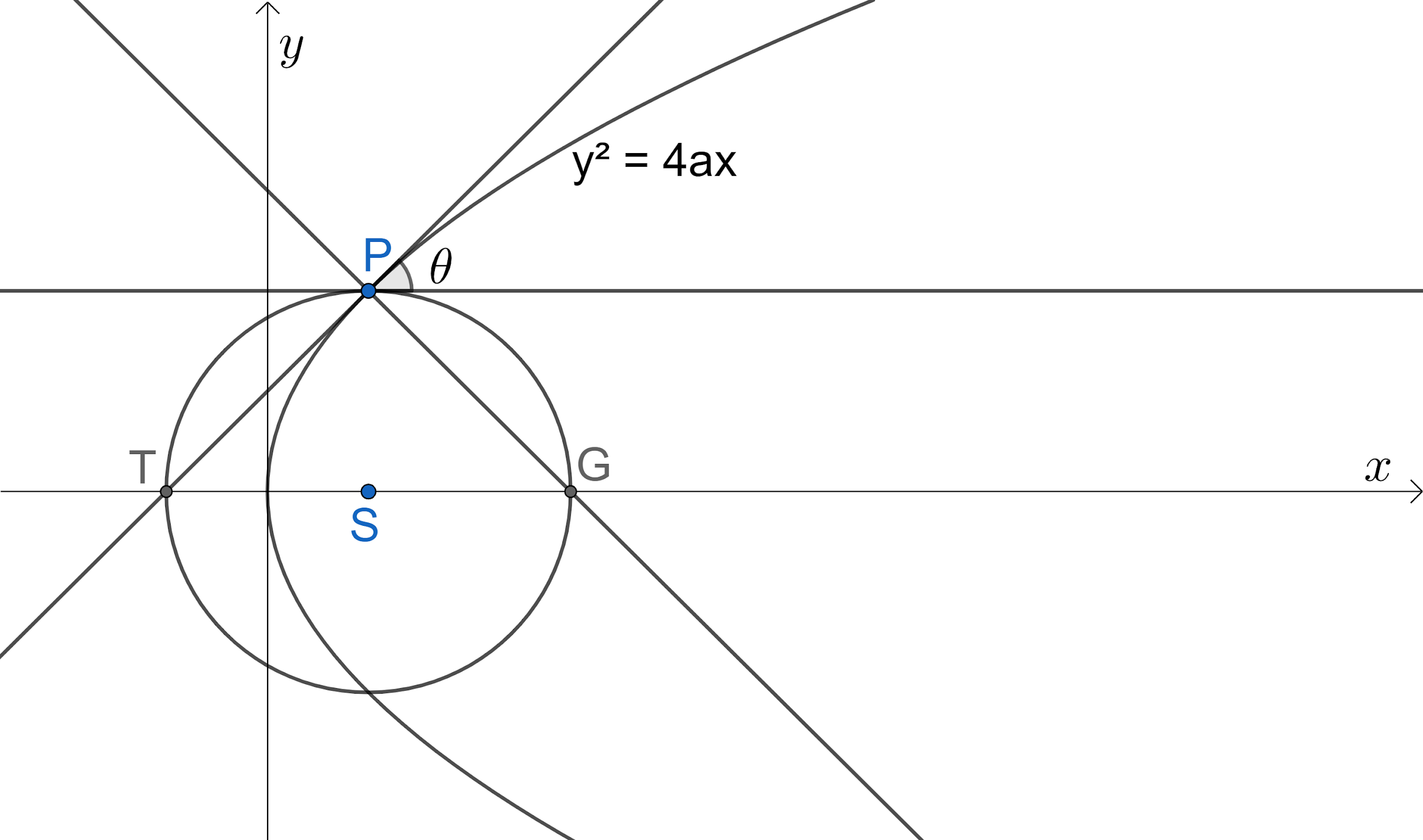
We first find the equation of the tangent and normal of the parabola ${{y}^{2}}=4ax$.
We know that the slope (m) of the tangent at any point $\left( x,y \right)$ to the curve y = f(x) is defined as $m={{\left. \dfrac{dy}{dx} \right|}_{\left( x,y \right)}}$.
Let the slope of the tangent to parabola be ${{m}_{1}}$.
So, let’s differentiate the curve ${{y}^{2}}=4ax$.
We know that $\dfrac{d}{dx}\left( {{x}^{n}} \right)=n.{{x}^{n-1}}$ and $\dfrac{d}{dx}\left( mx \right)=m$.
$\dfrac{d}{dx}\left( {{y}^{2}} \right)=\dfrac{d}{dx}\left( 4ax \right)$
$2y\dfrac{dy}{dx}=4a$.
$\dfrac{dy}{dx}=\dfrac{4a}{2y}$.
$\dfrac{dy}{dx}=\dfrac{2a}{y}$.
${{m}_{1}}={{\left. \dfrac{dy}{dx} \right|}_{p\left( a{{t}^{2}},2at \right)}}$.
${{m}_{1}}=\dfrac{2a}{2at}$.
${{m}_{1}}=\dfrac{1}{t}$ ---(1).
We have a tangent with slope ${{m}_{1}}=\dfrac{1}{t}$ and passing through $P\left( a{{t}^{2}},2at \right)$.
We know that equation of the straight line with slope ‘m’ and passing through $\left( {{x}_{1}},{{y}_{1}} \right)$ is $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$.
The equation of tangent at ‘P’ for parabola is $\left( y-2at \right)=\left( \dfrac{1}{t} \right)\times \left( x-a{{t}^{2}} \right)$.
$\left( y-2at \right)\times t=1\times \left( x-a{{t}^{2}} \right)$.
$yt-2a{{t}^{2}}=x-a{{t}^{2}}$.
$yt=x-a{{t}^{2}}+2a{{t}^{2}}$.
$yt=x+a{{t}^{2}}$.
The equation of the tangent at point P to the parabola is $yt=x+a{{t}^{2}}$ ---(2).
If the tangent $yt=x+a{{t}^{2}}$ touches x-axis, then y = 0.
So, we get $0.t=x+a{{t}^{2}}$.
$0=x+a{{t}^{2}}$.
\[x=-a{{t}^{2}}\].
So, tangent $yt=x+a{{t}^{2}}$ touches the x-axis at $T\left( -a{{t}^{2}},0 \right)$.
We know that the normal of parabola at P is perpendicular to the tangent $yt=x+a{{t}^{2}}$.
We know that the product of slopes of two perpendicular (non-vertical) lines is ‘-1’. Let us assume the slope of the normal be ${{m}_{2}}$.
We have ${{m}_{1}}.{{m}_{2}}=-1$.
$\dfrac{1}{t}.{{m}_{2}}=-1$.
${{m}_{2}}=-t$.
We have a normal with slope ${{m}_{2}}=-t$ and passing through $P\left( a{{t}^{2}},2at \right)$.
We know that equation of the straight line with slope ‘m’ and passing through $\left( {{x}_{1}},{{y}_{1}} \right)$ is $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$.
The equation of normal at ‘P’ for parabola is $\left( y-2at \right)=\left( -t \right)\times \left( x-a{{t}^{2}} \right).$
$y-2at=-tx+a{{t}^{3}}$.
$y=-tx+2at+a{{t}^{3}}$.
The equation of the normal at point P to the parabola is $y=-tx+2at+a{{t}^{3}}$ ---(3).
If the normal $y=-tx+2at+a{{t}^{3}}$ touches x-axis, then y = 0.
So, we have $0=-tx+2at+a{{t}^{3}}$.
$tx=2at+a{{t}^{3}}$.
$x=\dfrac{2at+a{{t}^{3}}}{t}$.
$x=2a+a{{t}^{2}}$.
So, normal $y=-tx+2at+a{{t}^{3}}$ touches x-axis at $G\left( 2a+a{{t}^{2}},0 \right)$.
We have a circle passing through points $P\left( a{{t}^{2}},2at \right)$, $T\left( -a{{t}^{2}},0 \right)$ and $G\left( 2a+a{{t}^{2}},0 \right)$.
Let us find the midpoint of points $T\left( -a{{t}^{2}},0 \right)$ and $G\left( 2a+a{{t}^{2}},0 \right)$.
We know that midpoint of $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$.
Mid-point of $T\left( -a{{t}^{2}},0 \right)$ and $G\left( 2a+a{{t}^{2}},0 \right)$ is $\left( \dfrac{-a{{t}^{2}}+2a+a{{t}^{2}}}{2},\dfrac{0+0}{2} \right)$.
Mid-point of $T\left( -a{{t}^{2}},0 \right)$ and $G\left( 2a+a{{t}^{2}},0 \right)$ is $\left( \dfrac{2a}{2},\dfrac{0}{2} \right)$.
Mid-point of $T\left( -a{{t}^{2}},0 \right)$ and $G\left( 2a+a{{t}^{2}},0 \right)$ is $S\left( a,0 \right)$, Which is focus of the parabola.
We know that the normal of a parabola passes through the focus of the parabola.
Let us find distances SG and SP.
We know distances between points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$.
$SG=\sqrt{{{\left( 2a+a{{t}^{2}}-a \right)}^{2}}+{{\left( 0-0 \right)}^{2}}}$.
$SG=\sqrt{{{\left( a+a{{t}^{2}} \right)}^{2}}}$.
$SG=a+a{{t}^{2}}$.
Since S is midpoint of T and G SG = ST.
Now, $SP=\sqrt{{{\left( a{{t}^{2}}-a \right)}^{2}}+{{\left( 2at \right)}^{2}}}$.
$SP=\sqrt{{{a}^{2}}{{t}^{4}}+{{a}^{2}}-2{{a}^{2}}{{t}^{2}}+4{{a}^{2}}{{t}^{2}}}$.
$SP=\sqrt{{{a}^{2}}{{t}^{4}}+{{a}^{2}}+2{{a}^{2}}{{t}^{2}}}$.
\[SP=\sqrt{{{\left( a{{t}^{2}}+a \right)}^{2}}}\].
$SP=a+a{{t}^{2}}$.
We got SP = SG = ST and the circle is passing through P, G and T. So, the center of the circle is $S\left( a,0 \right)$.
We know that equation of a circle with center $\left( {{x}_{1}},{{y}_{1}} \right)$ and radius ‘r’ is ${{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}$
So, the equation of the circle is ${{\left( x-a \right)}^{2}}+{{\left( y-0 \right)}^{2}}={{\left( a+a{{t}^{2}} \right)}^{2}}$.
${{x}^{2}}-2ax+{{a}^{2}}+{{y}^{2}}={{a}^{2}}+{{a}^{2}}{{t}^{4}}+2{{a}^{2}}{{t}^{2}}$.
${{x}^{2}}-2ax+{{y}^{2}}={{a}^{2}}{{t}^{4}}+2{{a}^{2}}{{t}^{2}}$ ---(4).
Let us slope $\left( {{m}_{3}} \right)$ of the circle at $P\left( a{{t}^{2}},2at \right)$.
So, let’s differentiate the curve ${{x}^{2}}-2ax+{{y}^{2}}={{a}^{2}}{{t}^{4}}+2{{a}^{2}}{{t}^{2}}$.
$\dfrac{d}{dx}\left( {{x}^{2}}-2ax+{{y}^{2}} \right)=\dfrac{d}{dx}\left( {{a}^{2}}{{t}^{4}}+2{{a}^{2}}{{t}^{2}} \right)$.
We know that $\dfrac{d}{dx}\left( {{x}^{n}} \right)=n.{{x}^{n-1}}$ and $\dfrac{d}{dx}\left( mx \right)=m$.
$2x-2a+2y\dfrac{dy}{dx}=0$.
$2y\dfrac{dy}{dx}=2a-2x$.
$\dfrac{dy}{dx}=\dfrac{a-x}{y}$.
\[{{m}_{3}}={{\left. \dfrac{dy}{dx} \right|}_{P\left( a{{t}^{2}},2at \right)}}=\dfrac{a-a{{t}^{2}}}{2at}\].
${{m}_{3}}=\dfrac{1-{{t}^{2}}}{2t}$ ---(5).
We have slopes of tangents of parabola and the circle at point P is ${{m}_{1}}$ and ${{m}_{3}}$. We find the angle $\left( \theta \right)$, between them.
We know that the angle (r) between the lines whose slopes are ${{m}_{s}}$ and ${{m}_{p}}$.
$\tan \left( r \right)=\left| \dfrac{{{m}_{s}}-{{m}_{p}}}{1+{{m}_{s}}.{{m}_{p}}} \right|$.
So, $\tan \left( \theta \right)=\left| \dfrac{\dfrac{1}{t}-\dfrac{\left( 1-{{t}^{2}} \right)}{2t}}{1+\left( \dfrac{1}{t}\times \dfrac{1-{{t}^{2}}}{2t} \right)} \right|$.
$\tan \theta =\left| \dfrac{\dfrac{2-1+{{t}^{2}}}{2t}}{1+\dfrac{1-{{t}^{2}}}{2{{t}^{2}}}} \right|$.
\[\tan \theta =\left| \dfrac{\dfrac{1+{{t}^{2}}}{2t}}{\dfrac{2{{t}^{2}}+1-{{t}^{2}}}{2{{t}^{2}}}} \right|\].
\[\tan \theta =\left| \dfrac{1+{{t}^{2}}}{\dfrac{{{t}^{2}}+{{1}^{2}}}{t}} \right|\].
$\tan \theta =t$.
$\theta ={{\tan }^{-1}}\left( t \right)$.
∴ The angle at which the tangent at P to the parabola is inclined to the tangent at P to the circle is $\theta ={{\tan }^{-1}}\left( t \right)$.
So, the correct answer is “Option C”.
Note: We should do all calculations without mistakes as all the values are in variables not in constants. We need to remember that the focus of the parabola is $\left( a,0 \right)$, to minimize solving time. We can alternatively use ${{S}_{1}}=0$, to find the equation of tangents. Similarly, we can calculate $\sin 2\theta $ using the value of $\tan \theta $ to give the result in ${{\sin }^{-1}}$.
Complete step by step answer:
Given that we have a parabola ${{y}^{2}}=4ax$, the tangent and normal at the point $P\left( a{{t}^{2}},2at \right)$ to the parabola meets x-axis at the points T and G. We need to find the angle between tangent at P for parabola and tangent at P to the circle passing through P, T, G.
Let us draw the given information
We first find the equation of the tangent and normal of the parabola ${{y}^{2}}=4ax$.
We know that the slope (m) of the tangent at any point $\left( x,y \right)$ to the curve y = f(x) is defined as $m={{\left. \dfrac{dy}{dx} \right|}_{\left( x,y \right)}}$.
Let the slope of the tangent to parabola be ${{m}_{1}}$.
So, let’s differentiate the curve ${{y}^{2}}=4ax$.
We know that $\dfrac{d}{dx}\left( {{x}^{n}} \right)=n.{{x}^{n-1}}$ and $\dfrac{d}{dx}\left( mx \right)=m$.
$\dfrac{d}{dx}\left( {{y}^{2}} \right)=\dfrac{d}{dx}\left( 4ax \right)$
$2y\dfrac{dy}{dx}=4a$.
$\dfrac{dy}{dx}=\dfrac{4a}{2y}$.
$\dfrac{dy}{dx}=\dfrac{2a}{y}$.
${{m}_{1}}={{\left. \dfrac{dy}{dx} \right|}_{p\left( a{{t}^{2}},2at \right)}}$.
${{m}_{1}}=\dfrac{2a}{2at}$.
${{m}_{1}}=\dfrac{1}{t}$ ---(1).
We have a tangent with slope ${{m}_{1}}=\dfrac{1}{t}$ and passing through $P\left( a{{t}^{2}},2at \right)$.
We know that equation of the straight line with slope ‘m’ and passing through $\left( {{x}_{1}},{{y}_{1}} \right)$ is $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$.
The equation of tangent at ‘P’ for parabola is $\left( y-2at \right)=\left( \dfrac{1}{t} \right)\times \left( x-a{{t}^{2}} \right)$.
$\left( y-2at \right)\times t=1\times \left( x-a{{t}^{2}} \right)$.
$yt-2a{{t}^{2}}=x-a{{t}^{2}}$.
$yt=x-a{{t}^{2}}+2a{{t}^{2}}$.
$yt=x+a{{t}^{2}}$.
The equation of the tangent at point P to the parabola is $yt=x+a{{t}^{2}}$ ---(2).
If the tangent $yt=x+a{{t}^{2}}$ touches x-axis, then y = 0.
So, we get $0.t=x+a{{t}^{2}}$.
$0=x+a{{t}^{2}}$.
\[x=-a{{t}^{2}}\].
So, tangent $yt=x+a{{t}^{2}}$ touches the x-axis at $T\left( -a{{t}^{2}},0 \right)$.
We know that the normal of parabola at P is perpendicular to the tangent $yt=x+a{{t}^{2}}$.
We know that the product of slopes of two perpendicular (non-vertical) lines is ‘-1’. Let us assume the slope of the normal be ${{m}_{2}}$.
We have ${{m}_{1}}.{{m}_{2}}=-1$.
$\dfrac{1}{t}.{{m}_{2}}=-1$.
${{m}_{2}}=-t$.
We have a normal with slope ${{m}_{2}}=-t$ and passing through $P\left( a{{t}^{2}},2at \right)$.
We know that equation of the straight line with slope ‘m’ and passing through $\left( {{x}_{1}},{{y}_{1}} \right)$ is $\left( y-{{y}_{1}} \right)=m\left( x-{{x}_{1}} \right)$.
The equation of normal at ‘P’ for parabola is $\left( y-2at \right)=\left( -t \right)\times \left( x-a{{t}^{2}} \right).$
$y-2at=-tx+a{{t}^{3}}$.
$y=-tx+2at+a{{t}^{3}}$.
The equation of the normal at point P to the parabola is $y=-tx+2at+a{{t}^{3}}$ ---(3).
If the normal $y=-tx+2at+a{{t}^{3}}$ touches x-axis, then y = 0.
So, we have $0=-tx+2at+a{{t}^{3}}$.
$tx=2at+a{{t}^{3}}$.
$x=\dfrac{2at+a{{t}^{3}}}{t}$.
$x=2a+a{{t}^{2}}$.
So, normal $y=-tx+2at+a{{t}^{3}}$ touches x-axis at $G\left( 2a+a{{t}^{2}},0 \right)$.
We have a circle passing through points $P\left( a{{t}^{2}},2at \right)$, $T\left( -a{{t}^{2}},0 \right)$ and $G\left( 2a+a{{t}^{2}},0 \right)$.
Let us find the midpoint of points $T\left( -a{{t}^{2}},0 \right)$ and $G\left( 2a+a{{t}^{2}},0 \right)$.
We know that midpoint of $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$.
Mid-point of $T\left( -a{{t}^{2}},0 \right)$ and $G\left( 2a+a{{t}^{2}},0 \right)$ is $\left( \dfrac{-a{{t}^{2}}+2a+a{{t}^{2}}}{2},\dfrac{0+0}{2} \right)$.
Mid-point of $T\left( -a{{t}^{2}},0 \right)$ and $G\left( 2a+a{{t}^{2}},0 \right)$ is $\left( \dfrac{2a}{2},\dfrac{0}{2} \right)$.
Mid-point of $T\left( -a{{t}^{2}},0 \right)$ and $G\left( 2a+a{{t}^{2}},0 \right)$ is $S\left( a,0 \right)$, Which is focus of the parabola.
We know that the normal of a parabola passes through the focus of the parabola.
Let us find distances SG and SP.
We know distances between points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$.
$SG=\sqrt{{{\left( 2a+a{{t}^{2}}-a \right)}^{2}}+{{\left( 0-0 \right)}^{2}}}$.
$SG=\sqrt{{{\left( a+a{{t}^{2}} \right)}^{2}}}$.
$SG=a+a{{t}^{2}}$.
Since S is midpoint of T and G SG = ST.
Now, $SP=\sqrt{{{\left( a{{t}^{2}}-a \right)}^{2}}+{{\left( 2at \right)}^{2}}}$.
$SP=\sqrt{{{a}^{2}}{{t}^{4}}+{{a}^{2}}-2{{a}^{2}}{{t}^{2}}+4{{a}^{2}}{{t}^{2}}}$.
$SP=\sqrt{{{a}^{2}}{{t}^{4}}+{{a}^{2}}+2{{a}^{2}}{{t}^{2}}}$.
\[SP=\sqrt{{{\left( a{{t}^{2}}+a \right)}^{2}}}\].
$SP=a+a{{t}^{2}}$.
We got SP = SG = ST and the circle is passing through P, G and T. So, the center of the circle is $S\left( a,0 \right)$.
We know that equation of a circle with center $\left( {{x}_{1}},{{y}_{1}} \right)$ and radius ‘r’ is ${{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}$
So, the equation of the circle is ${{\left( x-a \right)}^{2}}+{{\left( y-0 \right)}^{2}}={{\left( a+a{{t}^{2}} \right)}^{2}}$.
${{x}^{2}}-2ax+{{a}^{2}}+{{y}^{2}}={{a}^{2}}+{{a}^{2}}{{t}^{4}}+2{{a}^{2}}{{t}^{2}}$.
${{x}^{2}}-2ax+{{y}^{2}}={{a}^{2}}{{t}^{4}}+2{{a}^{2}}{{t}^{2}}$ ---(4).
Let us slope $\left( {{m}_{3}} \right)$ of the circle at $P\left( a{{t}^{2}},2at \right)$.
So, let’s differentiate the curve ${{x}^{2}}-2ax+{{y}^{2}}={{a}^{2}}{{t}^{4}}+2{{a}^{2}}{{t}^{2}}$.
$\dfrac{d}{dx}\left( {{x}^{2}}-2ax+{{y}^{2}} \right)=\dfrac{d}{dx}\left( {{a}^{2}}{{t}^{4}}+2{{a}^{2}}{{t}^{2}} \right)$.
We know that $\dfrac{d}{dx}\left( {{x}^{n}} \right)=n.{{x}^{n-1}}$ and $\dfrac{d}{dx}\left( mx \right)=m$.
$2x-2a+2y\dfrac{dy}{dx}=0$.
$2y\dfrac{dy}{dx}=2a-2x$.
$\dfrac{dy}{dx}=\dfrac{a-x}{y}$.
\[{{m}_{3}}={{\left. \dfrac{dy}{dx} \right|}_{P\left( a{{t}^{2}},2at \right)}}=\dfrac{a-a{{t}^{2}}}{2at}\].
${{m}_{3}}=\dfrac{1-{{t}^{2}}}{2t}$ ---(5).
We have slopes of tangents of parabola and the circle at point P is ${{m}_{1}}$ and ${{m}_{3}}$. We find the angle $\left( \theta \right)$, between them.
We know that the angle (r) between the lines whose slopes are ${{m}_{s}}$ and ${{m}_{p}}$.
$\tan \left( r \right)=\left| \dfrac{{{m}_{s}}-{{m}_{p}}}{1+{{m}_{s}}.{{m}_{p}}} \right|$.
So, $\tan \left( \theta \right)=\left| \dfrac{\dfrac{1}{t}-\dfrac{\left( 1-{{t}^{2}} \right)}{2t}}{1+\left( \dfrac{1}{t}\times \dfrac{1-{{t}^{2}}}{2t} \right)} \right|$.
$\tan \theta =\left| \dfrac{\dfrac{2-1+{{t}^{2}}}{2t}}{1+\dfrac{1-{{t}^{2}}}{2{{t}^{2}}}} \right|$.
\[\tan \theta =\left| \dfrac{\dfrac{1+{{t}^{2}}}{2t}}{\dfrac{2{{t}^{2}}+1-{{t}^{2}}}{2{{t}^{2}}}} \right|\].
\[\tan \theta =\left| \dfrac{1+{{t}^{2}}}{\dfrac{{{t}^{2}}+{{1}^{2}}}{t}} \right|\].
$\tan \theta =t$.
$\theta ={{\tan }^{-1}}\left( t \right)$.
∴ The angle at which the tangent at P to the parabola is inclined to the tangent at P to the circle is $\theta ={{\tan }^{-1}}\left( t \right)$.
So, the correct answer is “Option C”.
Note: We should do all calculations without mistakes as all the values are in variables not in constants. We need to remember that the focus of the parabola is $\left( a,0 \right)$, to minimize solving time. We can alternatively use ${{S}_{1}}=0$, to find the equation of tangents. Similarly, we can calculate $\sin 2\theta $ using the value of $\tan \theta $ to give the result in ${{\sin }^{-1}}$.
Recently Updated Pages
How to find how many moles are in an ion I am given class 11 chemistry CBSE
Class 11 Question and Answer - Your Ultimate Solutions Guide
Identify how many lines of symmetry drawn are there class 8 maths CBSE
State true or false If two lines intersect and if one class 8 maths CBSE
Tina had 20m 5cm long cloth She cuts 4m 50cm lengt-class-8-maths-CBSE
Which sentence is punctuated correctly A Always ask class 8 english CBSE
Trending doubts
The reservoir of dam is called Govind Sagar A Jayakwadi class 11 social science CBSE
What problem did Carter face when he reached the mummy class 11 english CBSE
What organs are located on the left side of your body class 11 biology CBSE
Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE
Petromyzon belongs to class A Osteichthyes B Chondrichthyes class 11 biology CBSE
Comparative account of the alimentary canal and digestive class 11 biology CBSE