Question

The tension in the string in the pulley system shown in the figure is:

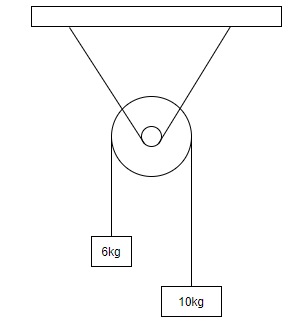
Answer 1

Hint: The given problem is an example of connected motion in which two bodies of different masses \[\mathop m\nolimits_1 \]and \[\mathop m\nolimits_2 \] are connected at the ends of an inextensible string and considered that this string passes over light and frictionless pulley.

Complete step by step solution:
Step 1:

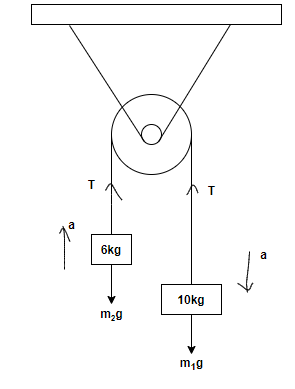
In the question it is given that one body is heavier than the other. So, let \[{m_1} > {m_2}\]where \[\mathop m\nolimits_1 = \]10kg and \[\mathop m\nolimits_2 = \]6kg.
Let \[a\]be the common acceleration of the system of two bodies as shown in the above figure.
Step 2: Since the pulley is light and frictionless, therefore, the tension in the string shall be the same on the both sides of the pulley as shown in the above figure.
Now we have to take the consideration of the forces working on the two bodies and these forces are as given below-
On the heavier body, the forces are:
Its weight \[{m_1}g\] acting downwards,
The tension \[T\] in the string working upwards.
As the body moves downwards with the acceleration \[a\], the net downward force on the body is \[{m_1}a\].
So, \[{m_1}g - T = {m_1}a\] …………………...(1)
On the lighter body, the forces are:
Its weight \[{m_2}g\] acting downwards,
The tension \[T\] in the string acting upwards.
As the body moves upwards with the acceleration \[a\], the net upward force on the body is \[{m_2}a\].
So, \[T - {m_2}g = {m_2}a\]...................... (2)
Step 3: Tension \[T\] in the string can be calculated by dividing equation (1) by (2),
We get, \[\dfrac{{{m_1}g - T}}{{T - {m_2}g}} = \dfrac{{{m_1}a}}{{{m_2}a}}\]
 \[\dfrac{{{m_1}g - T}}{{T - {m_2}g}} = \dfrac{{{m_1}}}{{{m_2}}}\]
\[{m_1}{m_2}g - {m_2}T = {m_1}T - {m_2}{m_1}g\]
\[{m_1}{m_2}g + {m_1}{m_2}g = {m_1}T + {m_2}T\]
\[2{m_1}{m_2}g = ({m_1} + {m_2})T\]
\[T = \dfrac{{2{m_1}{m_2}g}}{{({m_1} + {m_2})}}\] ……………... (3)
From the question, values of masses of the bodies and the acceleration due to gravity i.e. \[g = \]10m/s can be kept in the equation (3) and tension \[T\] can be calculated as-
 \[T = \dfrac{{2 \times 10 \times 6 \times 10}}{{(10 + 6)}}\]
 \[T = \dfrac{{1200}}{{16}}\]
\[T = 75\]N.

The correct option is (A).

Note:
(i) While solving these types of questions balancing the force equations is a must. The force in which direction the body is moving is higher than the opposite force working on the body.
(ii) If there is nothing mentioned about the weight and friction of the pulley then it should be considered light and frictionless respectively.
(iii) And if the pulley is lightweight and frictionless then tension \[T\] will be the same on both sides of the pulley.