Question

The three vertices of a parallelogram are (3, 4), (3, 8) and (9, 8). Find the fourth vertex.

Answer 1

Hint: Assume the coordinate of the fourth vertex of parallelogram ABCD to be (x,y). We know that the diagonal of a parallelogram bisects each other. Since ABCD is a parallelogram, the diagonals must bisect each other. We know that the midpoint(x,y) of A \[({{x}_{1}},{{y}_{1}})\] and B \[({{x}_{2}},{{y}_{2}})\] is \[x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}\] , \[y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}\] . Using the midpoint formula, find the coordinate of the midpoint of the diagonal BD. Similarly, find the midpoint of the coordinate of the diagonal AC. Since the diagonals meet at a point O. So, the midpoint of the diagonal AC and the diagonal BD must coincide. Now, solve it further and get the values of x and y.

Complete step-by-step answer:

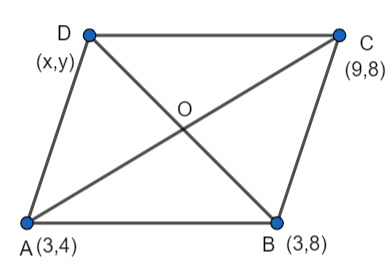
Let the coordinate of the fourth vertex D be (x,y).
We know that the diagonals of a parallelogram bisect each other. Since ABCD is a parallelogram, the diagonals must bisect each other.
For diagonal AC, O is its midpoint.
We know the formula that the midpoint(x,y) of A \[({{x}_{1}},{{y}_{1}})\] and B \[({{x}_{2}},{{y}_{2}})\] is \[x=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}\] , \[y=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}\] .
As O is the midpoint of the diagonal AC, we can find its coordinates using the midpoint formula.
We have, A = (3,4) and C = (9,8),
O = \[\left( \dfrac{3+9}{2},\dfrac{4+8}{2} \right)\] = \[\left( 6,6 \right)\] ……………………….(1)
As O is the midpoint of the diagonal BD, we can find its coordinates using the midpoint formula.
We have, B = (3,8) and D = (x,y),
O = \[\left( \dfrac{3+x}{2},\dfrac{8+y}{2} \right)\] …………………….(2)
Comparing equation (1) and equation (2), we get
\[6=\dfrac{3+x}{2}\] ………………….(3)
\[6=\dfrac{8+y}{2}\] ………………….(4)
Solving equation (3), we get
\[\begin{align}
  & 6=\dfrac{3+x}{2} \\
 & \Rightarrow 12=3+x \\
 & \Rightarrow 9=x \\
\end{align}\]
Solving equation (4), we get
\[\begin{align}
  & 6=\dfrac{8+y}{2} \\
 & \Rightarrow 12=8+y \\
 & \Rightarrow 4=y \\
\end{align}\]
The values of x and y are 4 and 9 respectively.
So, D = (9,4).
Hence, the fourth vertex is (9,4).

Note: We can also solve this question using the distance formula.

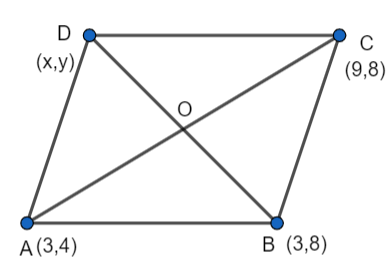
Let the fourth vertex of the parallelogram be (x,y).
We know that the opposite sides of a parallelogram are equal to each other.
So, AB = CD and BC = AD.
AB = \[\sqrt{{{(3-3)}^{2}}+{{(4-8)}^{2}}}=4\] …………………(1)
BC = \[\sqrt{{{(3-9)}^{2}}+{{(8-8)}^{2}}}=6\] ……………………..(2)
CD = \[\sqrt{{{(9-x)}^{2}}+{{(8-y)}^{2}}}=\sqrt{{{x}^{2}}+{{y}^{2}}-18x-16y+145}\] ………………………(3)
AD = \[\sqrt{{{(3-x)}^{2}}+{{(4-y)}^{2}}}=\sqrt{{{x}^{2}}+{{y}^{2}}-6x-8y+25}\] ……………………..(4)
From equation (1) and equation (3), we get
\[A{{B}^{2}}=C{{D}^{2}}\]
\[{{4}^{2}}={{x}^{2}}+{{y}^{2}}-18x-16y+145\] …………………..(5)
From equation (2) and equation (4), we get
\[B{{C}^{2}}=A{{D}^{2}}\]
\[{{6}^{2}}={{x}^{2}}+{{y}^{2}}-6x-8y+25\] …………………..(6)
We have two equations and two variables. On solving equation (5) and equation (6), we get
x=9 and y=4.
Hence, the fourth vertex is (9,4).