Question

The top of a broken tree has it’s top-end touching the ground at a distance 15m from the bottom, the angle made by the broken end with the ground is ${30^\circ }$. Then the length of the broken part is.
A) ${\text{10m}}$
B) $\sqrt {\text{3}} {\text{m}}$
C) ${\text{5}}\sqrt {\text{3}} {\text{m}}$
D) ${\text{10}}\sqrt {\text{3}} {\text{m}}$

Answer 1

Hint: We can draw a diagram with the given details. Then we can form a trigonometric ratio and solve the equation to get the required length. According to the question the, appropriate trigonometric ratio will be tan.

Complete step by step solution: We can draw a diagram with the given details

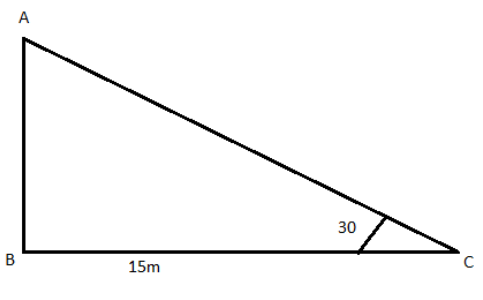
In the figure, AC is the broken part of the tree, B is the foot of the tree and c is the point where the top end touches the ground.
Consider right triangle ABC, by trigonometry,
${\text{cosC = }}\dfrac{{{\text{adjecent side}}}}{{{\text{hypotenuse}}}}{\text{ = }}\dfrac{{{\text{BC}}}}{{{\text{AC}}}}$
${\text{cos30 = }}\dfrac{{{\text{15}}}}{{{\text{AB}}}}$
We know ${\text{cos30 = }}\dfrac{{\sqrt {\text{3}} }}{{\text{2}}}$. Using this in the above equation, we get,
$\dfrac{{\sqrt {\text{3}} }}{{\text{2}}}{\text{ = }}\dfrac{{{\text{15}}}}{{{\text{AB}}}}$
\[
   \Rightarrow {\text{AB = }}\dfrac{{{\text{15} \times 2}}}{{\sqrt {\text{3}} }}{\text{ = }}\dfrac{{{\text{30}}}}{{\sqrt {\text{3}} }} \\
   \Rightarrow {\text{AB = 10}}\sqrt {\text{3}} {\text{ m}} \\
  \]
So, length of the broken part is \[{\text{10}}\sqrt {\text{3}} {\text{ m}}\]

Therefore, the correct answer is option D.

Note: Drawing a diagram with the given details is very important. The concept of simple trigonometry is used to find the length of the broken piece. Trigonometric values of important angles must be known. We must understand which angle and sides of the right-angled triangle are given in the question.