
The transverse axis of a hyperbola is of length 2a and a vertex divides the segment of the axis between the centre and the corresponding focus in the ratio 2:1. The equation of the hyperbola is
Answer
526.2k+ views
Hint-In this question, we use the property of the hyperbola. We know the eccentricity of hyperbola
Complete step-by-step answer:
Given, length of transverse axis is 2a so the length of semi transverse axis is a.
Let equation of hyperbola is
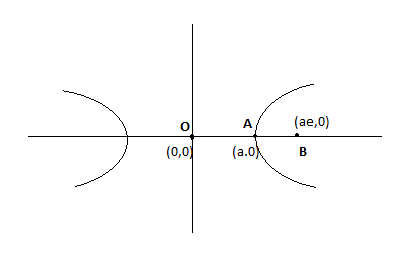
From figure, coordinate of vertex A(a, 0), Focus B(ae, 0) and centre O(0, 0).
Now, vertex A (a, 0) divides the line joining between focus B (ae, 0) and centre O (0, 0) in the ratio 2:1.
We have to apply section formula,
Now, use
Squaring both sides,
Cross multiplication,
Put the value of b2 in (1) equation,
Hence, the equation of hyperbola is
So, the correct option is (d).
Note- In such types of problems we should remember the coordinates of vertex, Focus and centre of hyperbola and then find the value of eccentricity with the help of these coordinates and section formula. Then after using the eccentricity formula we can easily make a relation between a and b.
Complete step-by-step answer:
Given, length of transverse axis is 2a so the length of semi transverse axis is a.
Let equation of hyperbola is
From figure, coordinate of vertex A(a, 0), Focus B(ae, 0) and centre O(0, 0).
Now, vertex A (a, 0) divides the line joining between focus B (ae, 0) and centre O (0, 0) in the ratio 2:1.
We have to apply section formula,
Now, use
Squaring both sides,
Cross multiplication,
Put the value of b2 in (1) equation,
Hence, the equation of hyperbola is
So, the correct option is (d).
Note- In such types of problems we should remember the coordinates of vertex, Focus and centre of hyperbola and then find the value of eccentricity with the help of these coordinates and section formula. Then after using the eccentricity formula we can easily make a relation between a and b.

Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




