Question

The two adjacent sides of a cyclic quadrilateral are 2 and 5 and the angle between them is ${{60}^{\circ }}$. If the area of the quadrilateral is $4\sqrt{3}$, find the remaining two sides.\[\]

Answer 1

Hint: Draw a diagram of the given cyclic quadrilateral and assign all the given data in the question. Use the law of sine and cosine rule to find out the length of other sides.

Complete step by step answer:
We know that the cyclic quadrilateral is inscribed within a circle or the vertices of a cyclic quadrilateral lies on a circle. We also know that the sum of opposite angles in a quadrilateral is ${{180}^{\circ }}$. So the angle opposite to ${{60}^{\circ }}$ will be ${{180}^{\circ }}-{{60}^{\circ }}={{120}^{\circ }}$\[\]

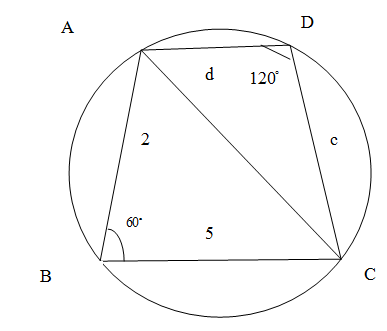
We draw diagram of the given cyclic quadrilateral $ABCD$ where we assign the angles $\angle ABC={{60}^{\circ }}$ and $\angle ADC={{60}^{\circ }}$. We assign the given lengths and unknown lengths of four t sides to $AB=5,BC=2,CD=c,DA=d$.\[\]
We know from the sine rule that area of a triangle with lengths with two sides $a,b$ and the angle made by them $\angle ABC$ is given by ,
\[\Delta =\dfrac{1}{2}ab\sin \left( \angle ABC \right)...(1)\]
Putting in equation(1) $b=AB=5,a=BC=2,\angle ABC={{60}^{\circ }}$we get area of the triangle $ABC$
\[{{\Delta }_{1}}=\dfrac{1}{2}ab\sin \left( \angle ABC \right)=\dfrac{1}{2}\left( 5\cdot 2\cdot \dfrac{\sqrt{3}}{2} \right)=\dfrac{5\sqrt{3}}{2}\]
Similarly the area of the triangle $ADC$ is ,
\[{{\Delta }_{1}}=\dfrac{1}{2}cd\sin \left( \angle ADC \right)=\dfrac{1}{2}\left( cd\dfrac{\sqrt{3}}{2} \right)=\dfrac{cd\sqrt{3}}{4}\]
It is also given that the area of the quadrilateral $ ABCD$ is $\Delta =4\sqrt{3}$ but the area of quadrilateral $ABCD$ is the sum of area of the triangle $ABC$ and area of the triangle $ADC$. So,
\[\begin{align}
  & \Delta ={{\Delta }_{1}}+{{\Delta }_{2}} \\
 & \Rightarrow 4\sqrt{3}=\dfrac{5\sqrt{3}}{2}+\dfrac{cd\sqrt{3}}{4} \\
 & \Rightarrow cd=16-10=6 \\
\end{align}\]

We also know from the cosine rule that the relation in the triangle $ABC$ among three sides $AB,BC,AC$ and the angle made by $AB,BC=\angle ABC$ is given by ,
\[A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}-2AB\cdot BC\cos \left( \angle ABC \right)...(2)\]
Similarly in the triangle $ADC$
\[A{{C}^{2}}=A{{D}^{2}}+C{{D}^{2}}-2AD\cdot CD\cos \left( \angle ADC \right)...(3)\]
So we equate right hand side of equation (2) and (3) and put known values
\[\begin{align}
  & A{{B}^{2}}+B{{C}^{2}}-2AB\cdot BC\cos \left( \angle ABC \right)=A{{D}^{2}}+C{{D}^{2}}-2AD\cdot CD\cos \left( \angle ADC \right) \\
 & \Rightarrow {{2}^{2}}+{{5}^{2}}-2\left( 2 \right)\left( 5 \right)\cos \left( {{60}^{\circ }} \right)={{d}^{2}}+{{c}^{2}}-2cd\cos \left( {{120}^{\circ }} \right) \\
 & \Rightarrow 19={{d}^{2}}+{{c}^{2}}+cd \\
 & \Rightarrow {{d}^{2}}+{{c}^{2}}=13\left( \because cd=6 \right) \\
\end{align}\]
We obtained that ${{d}^{2}}+{{c}^{2}}=13,{{c}^{2}}{{d}^{2}}=36$. So we form the quadratic equation in $x$ whose roots are ${{c}^{2}},{{d}^{2}}$ and solve it by splitting the middle term method
\[\begin{align}
  & {{x}^{2}}-\left( {{c}^{2}}+{{d}^{2}} \right)x+cd=0 \\
 & \Rightarrow {{x}^{2}}-13x+36=0 \\
 & \Rightarrow \left( x-9 \right)\left( x-4 \right)=0 \\
 & \Rightarrow x=9\text{ or }x=4 \\
\end{align}\]
Now ${{c}^{2}}=9,{{d}^{2}}=4$ or ${{c}^{2}}=4,{{d}^{2}}=9$. We reject the negative values for distances to get $c=3,d=2\text{ or }c=2,d=3$. \[\]

So the length of other two sides are 2 and 3.

Note: The question tests your knowledge of cyclic quadrilateral, sine rule and cosine rule. Careful solving of simultaneous equations with substitution and usage of formula will lead us to arrive at the correct result. The question can also be reframed to find the rest of the angles.