Question

The two legs of a right triangle are equal and the square of its hypotenuse is 50. Find the length of each leg.

Answer 1

Hint – In this question first draw the pictorial representation of the right angle triangle and mark all the points it will give us a clear picture what we have to find out, later on in the solution apply the Pythagoras theorem which will help us to find out the length of the other two legs of the right triangle (as hypotenuse length is given).

Complete step-by-step answer:

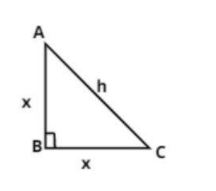
The right angle triangle ABC is shown above having right angle at B as shown in the figure.
It is given that the length of the two legs of a right angle triangle are equal and the square of its hypotenuse is 50 .
Let the length of the two legs be x as shown in the figure.
AB = BC = x.
Let the hypotenuse of a right angle triangle ABC be h.
$ \Rightarrow {h^2} = 50$.
$ \Rightarrow {\left( {AC} \right)^2} = {h^2} = 50$.
Now using Pythagora's theorem (i.e. the sum of the squares of the legs of the right angle triangle is equal to the square of the hypotenuse of the right angle triangle).
Therefore, ${\left( {{\text{perpendicular}}} \right)^2} + {\left( {{\text{base}}} \right)^2} = {\left( {{\text{hypotenuse}}} \right)^2}$
Now substitute the values in the above equation we have,
$ \Rightarrow {\left( {{\text{AB}}} \right)^2} + {\left( {{\text{BC}}} \right)^2} = {\left( {{\text{AC}}} \right)^2}$
Now again substitute the values in the above equation we have,
$ \Rightarrow {\left( {\text{x}} \right)^2} + {\left( {\text{x}} \right)^2} = {\left( {\text{h}} \right)^2}$
Now again substitute the values in the above equation we have,
$ \Rightarrow {\left( {\text{x}} \right)^2} + {\left( {\text{x}} \right)^2} = 50$
$ \Rightarrow 2{x^2} = 50$
Now divide by 2 throughout we have,
$ \Rightarrow {x^2} = \dfrac{{50}}{2} = 25$
Now take the square root of the given equation we have,
$ \Rightarrow \sqrt {{x^2}} = \sqrt {25} $
$ \Rightarrow x = \pm 5$
As length cannot be negative so x = 5
So the length of the two legs of the right angle triangle is 5.
So this is the required answer.

Note – Whenever we face such types of question always assume any variable be the length of the leg of the right triangle and it is given that the two legs of the right triangle are of same length so the length of the other leg also be the same variable which we assumed then apply the Pythagoras theorem as above and simplify we will get the required lengths of the other two legs of the right angle triangle.