
The upper half of an inclined plane with inclination
(A).
(B).
(C).
(D).
Answer
464.1k+ views
Hint: The first part of the inclined plane is smooth so o frictional force will act when the body moving through the upper half but lower half is rough due to which frictional force comes into play. Draw a FBD diagram of the body and resolve the forces into its components. Solve forces acting in different directions on the body. Using equations of motion and Newton’s second law, we can calculate the coefficient of friction.
Formula used:
Complete answer:
Given, a body is coming down an inclined plane inclined at an angle
The FBD diagram for the body will be-
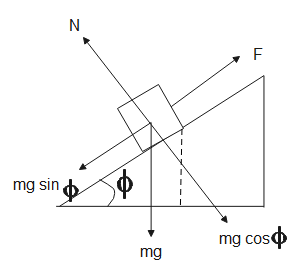
In the figure shown, the body is halfway through the inclined plane, let the length of the incline be
The acceleration of the body in the first half is
Applying equation of motion-
Here,
Substituting values in the above equation, we get,
Therefore, the velocity of the body just before it starts moving through the second half is
In the second half, the forces acting on the body will be-
Here,
From the figure,
Substituting in the above equation, we get,
Therefore, the acceleration of the body when it is coming down the second half is
Therefore, the value of coefficient of friction is
For the lower half, the coefficient of friction is
Hence, the correct option is (A).
Note:
According to Newton’s second law of motion, a body undergoes acceleration when there is external force acting on it otherwise it moves with uniform motion or remains at rest. The force that opposes the motion of a body is frictional force. Since, the upper half is smooth, no frictional force acts on the body, the lower half is rough and interlocking of irregularities takes place due to which frictional force comes into play.
Formula used:
Complete answer:
Given, a body is coming down an inclined plane inclined at an angle
The FBD diagram for the body will be-

In the figure shown, the body is halfway through the inclined plane, let the length of the incline be
The acceleration of the body in the first half is
Applying equation of motion-
Here,
Substituting values in the above equation, we get,
Therefore, the velocity of the body just before it starts moving through the second half is
In the second half, the forces acting on the body will be-
Here,
From the figure,
Substituting in the above equation, we get,
Therefore, the acceleration of the body when it is coming down the second half is
Therefore, the value of coefficient of friction is
For the lower half, the coefficient of friction is
Hence, the correct option is (A).
Note:
According to Newton’s second law of motion, a body undergoes acceleration when there is external force acting on it otherwise it moves with uniform motion or remains at rest. The force that opposes the motion of a body is frictional force. Since, the upper half is smooth, no frictional force acts on the body, the lower half is rough and interlocking of irregularities takes place due to which frictional force comes into play.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




