Question

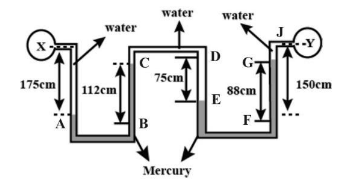
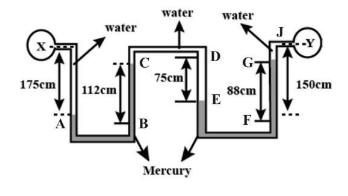
: The U-tube manometers are connected to the same tube as shown in figure. Determine difference of pressure between $X$and $Y$. Take specific gravity of mercury as $13.6(g = 10m/{s^2},{P_{Hg}} = 13600kg/{m^2})$

Answer 1

Hint: Convert the pressure in terms of one fluid: either water or mercury, then start from X and go till Y. Keep on adding pressure while going downwards and subtracting while going upwards.

Complete step by step answer:

First of all let us do conversion from Mercury pressure to water pressure:
\[P = {D_w} \times g\, \times {H_w}\;\]………….(1)
\[P = {D_{Hg}} \times g \times \,{H_g}\;\]……….(2)
As we want to find equivalent pressure of water and Mercury so let us equate (1) and (2 )
\[{D_w} \times g \times {H_w} = {D_{Hg}} \times g \times {H_{Hg\;\;}}\;\]………… (3)
\[{H_w} = \;{H_{HG}}\; \times \;\;\dfrac{{{D_{HG}}}}{{{D_w}}}\]
\[{H_w}\; = \;{H_{HG}}\; \times \;\dfrac{{{D_{HG}}}}{{{D_w}}}{H_w}\; = \;{H_{HG}} \times \;\dfrac{{{D_{HG}}}}{{{D_w}}}\]
Now it is given that \[\dfrac{{{D_{HG}}}}{{{D_w}}}\], the specific gravity of mercury is\[13.6\].
\[Hw = 13.6{\text{ }}{H_{HG}}\]………… (4)
Now start from $X$, first we get \[175{\text{ }}cm\]of water column so total pressure till here is
\[Px + 175{\text{ }}cm\]
Then from \[A{\text{ }}to{\text{ }}B\;\]pressure gets cancelled out .
Now let us convert \[112{\text{ }}cm\]mercury column pressure from \[B{\text{ }}to{\text{ }}C\]into water column pressure. \[\left( {112 \times 13.6} \right)\]
So till point C here pressure becomes \[Px + 175-112 \times 13.6\]
From \[C\,to\,D\] pressure is equal so it cancels out.
From \[D{\text{ }}to{\text{ }}E{\text{ }}75cm\]of water pressure is added.
Total till E pressure becomes \[Px + 175-112{\text{ }} \times 13.6 + 75\]
Now we see that Pressure from \[E{\text{ }}to{\text{ }}F\]cancels out as these are equal.
From \[F{\text{ }}to{\text{ }}G\]Convert mercury pressure to water pressure \[\left( {88 \times 13.6} \right)\]and it is to be subtracted.
So pressure till G becomes \[Px + 175-112 \times 13.6 + 75 - 88 \times 13.6\]
Now the water column of\[\;\left( {150 - 88 = 62} \right)\]from G to J is to be subtracted.
So total pressure till Y becomes \[Px + 175-112 \times 13.6 + 75 - 88 \times 13.6-62 = Py\]
So,\[Px-Py\; = 2532cm\]
\[ = D\;gH\]
\[ = 1000 \times 10 \times 2532 \times {10^{ - 2}}\]
\[ = \;253200N/{m^2}\]
So, Difference in pressure between points \[X{\text{ }}and{\text{ }}Y{\text{ }}is{\text{ }}253200N/{m^2}\]
First of all let us do conversion from Mercury pressure to water pressure:
\[P = {D_w} \times g\, \times {H_w}\;\]………….(1)
\[P = {D_{Hg}} \times g \times \,{H_g}\;\]……….(2)
As we want to find equivalent pressure of water and Mercury so let us equate (1) and (2 )
\[{D_w} \times g \times {H_w} = {D_{Hg}} \times g \times {H_{Hg\;\;}}\;\]………… (3)
\[{H_w} = \;{H_{HG}}\; \times \;\;\dfrac{{{D_{HG}}}}{{{D_w}}}\]
\[{H_w}\; = \;{H_{HG}}\; \times \;\dfrac{{{D_{HG}}}}{{{D_w}}}{H_w}\; = \;{H_{HG}} \times \;\dfrac{{{D_{HG}}}}{{{D_w}}}\]
Now it is given that \[\dfrac{{{D_{HG}}}}{{{D_w}}}\], the specific gravity of mercury is\[13.6\].
\[Hw = 13.6{\text{ }}{H_{HG}}\]………… (4)
Now start from $X$, first we get \[175{\text{ }}cm\]of water column so total pressure till here is
\[Px + 175{\text{ }}cm\]
Then from \[A{\text{ }}to{\text{ }}B\;\]pressure gets cancelled out .
Now let us convert \[112{\text{ }}cm\]mercury column pressure from \[B{\text{ }}to{\text{ }}C\]into water column pressure. \[\left( {112 \times 13.6} \right)\]
So till point C here pressure becomes \[Px + 175-112 \times 13.6\]
From \[C\,to\,D\] pressure is equal so it cancels out.
From \[D{\text{ }}to{\text{ }}E{\text{ }}75cm\]of water pressure is added.
Total till E pressure becomes \[Px + 175-112{\text{ }} \times 13.6 + 75\]
Now we see that Pressure from \[E{\text{ }}to{\text{ }}F\]cancels out as these are equal.
From \[F{\text{ }}to{\text{ }}G\]Convert mercury pressure to water pressure \[\left( {88 \times 13.6} \right)\]and it is to be subtracted.
So pressure till G becomes \[Px + 175-112 \times 13.6 + 75 - 88 \times 13.6\]
Now the water column of\[\;\left( {150 - 88 = 62} \right)\]from G to J is to be subtracted.
So total pressure till Y becomes \[Px + 175-112 \times 13.6 + 75 - 88 \times 13.6-62 = Py\]
So,\[Px-Py\; = 2532cm\]
\[ = D\;gH\]
\[ = 1000 \times 10 \times 2532 \times {10^{ - 2}}\]
\[ = \;253200N/{m^2}\]
So, Difference in pressure between points \[X{\text{ }}and{\text{ }}Y{\text{ }}is{\text{ }}253200N/{m^2}\]

Note:Remember that different liquids have different pressures even if column lengths are the same. Alternate way of solution is to calculate the absolute value of pressure in each part and then add and subtract for downward and upward pressure respectively.