Question

The value of $\dfrac{{\tan {{245}^\circ } + \tan {{335}^\circ }}}{{\tan {{205}^\circ } + \tan {{115}^\circ }}}$ is equal to

Answer 1

Hint: Here, simplify the angles for tangents given in simplified form using circular trigonometry rules. Then we will perform the basic algebraic calculation to get the result.

Complete step by step answer:
The given expression is $\dfrac{{\tan {{245}^\circ } + \tan {{335}^\circ }}}{{\tan {{205}^\circ } + \tan {{115}^\circ }}}$.
To find the value of the trigonometric terms above, we will use quadrant concepts of trigonometry.
We can see each trigonometric term sign in the below figure.

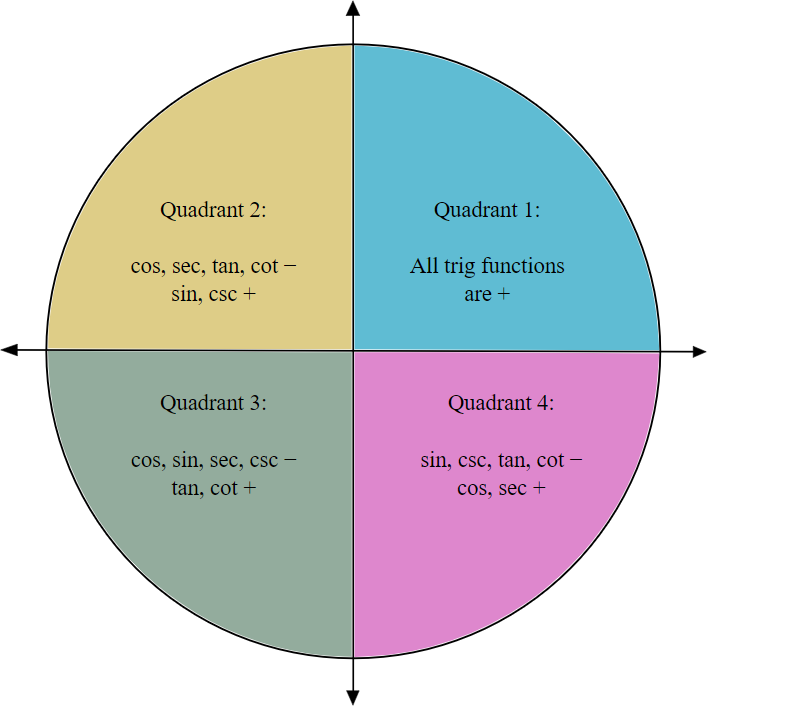
As we know that the function tangent is positive in the first and third quadrant and the function remains the same for angles $180^\circ$ and $360^\circ$.
Writing the angles in the sum of either $180^\circ$ or $360^\circ$ to change the values into simplified form,
$tan (245^\circ) = tan (180^\circ + 65^\circ) = tan (65^\circ)$
$tan (335^\circ) = tan (360^\circ – 25^\circ) = – tan (25^\circ)$
$tan (205^\circ) = tan (180^\circ + 25^\circ) = tan (25^\circ)$
$tan (115^\circ) = tan (180^\circ – 65^\circ) = – tan (65^\circ)$
Substituting these values in the given expression, we get
$\Rightarrow \dfrac{{\tan {{65}^\circ } - \tan {{25}^\circ }}}{{\tan {{25}^\circ } - \tan {{65}^\circ }}}$= – 1

Therefore, the value of $\dfrac{{\tan {{245}^\circ } + \tan {{335}^\circ }}}{{\tan {{205}^\circ } + \tan {{115}^\circ }}}$ is – 1.

Note:
In these types of questions, do not go for direct calculation. Always change the angles, so that all angles become less than equal to $90^\circ$. If you get any standard value, then put the values and if not then simplify the obtained terms using trigonometry rules. For doing these types of questions related to bigger angles, you must use the angles conversion rules of circular trigonometry i.e., how angles and trigonometric tools change with angles of $90^\circ, 180^\circ, 270^\circ$, and $360^\circ$. You must know that we can calculate values of trigonometric tools with large angels by changing them to angles equal to or below $90^\circ$.