Question

The value of gravitational constant G was first experimentally determined by:
A) Galileo
B) Newton
C) Cavendish
D) Kelvin

Answer 1

Hint: The value of gravitational constant, G first determined was $6.75 \times {10^{ - 11}}N{m^2}k{g^{ - 2}}$.

Complete step by step answer:
After nearly a century in 1798, Lord Henry Cavendish came to determine the value for that constant G by the experiment of torsional balance.

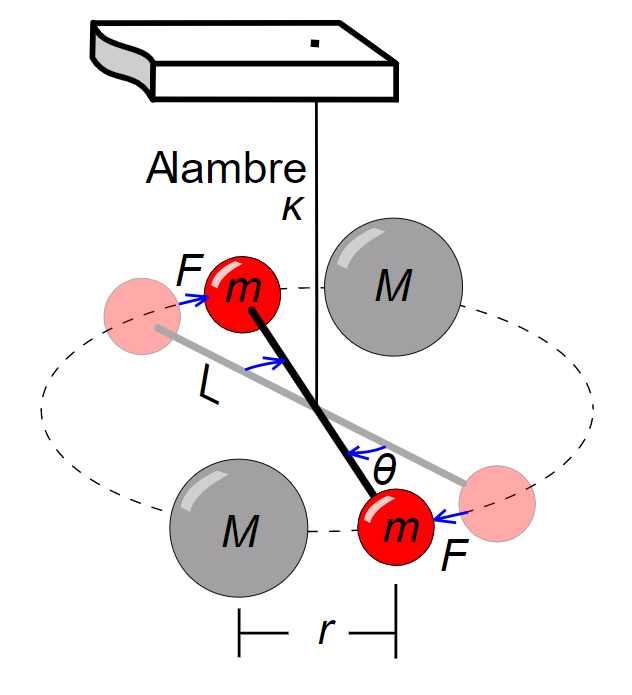
He attached the two small lead spheres in each side of the rod and the rod was suspended by a thin wire. When the rod is twisted, the torsion of the wire begins to exert the torsional force which is proportional to the angle of rotation. Then the more twisting leads the system to restore itself backward more. By this, Cavendish calculated the relationship between the angle of rotation to the amount of torsional force.
And then he brought two large spheres near to the small lead spheres connected to the rod. The large spheres exert the gravitational force on the small spheres which causes the rod to twist. Once the torsional force equals the gravitational force, the twisting stops. The rod comes to rest. Using this, Cavendish calculated the force of attraction. Then finally he determined the value of G.
Cavendish determined G as $6.75 \times {10^{ - 11}}N{m^2}k{g^{ - 2}}$. Now the accepted value is $6.67 \times {10^{ - 11}}N{m^2}k{g^{ - 2}}$

$\therefore $ The correct option is option (C).

Additional information:
(i)Sir Issac Newton in 1687, in his book philosophiae Naturalis Principia Mathematica discovered the term Gravitational constant for the first time while explaining the gravitational force.
(ii)Newton states that the gravitational force between any two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centres.
$\therefore {F_{grav}}\alpha \dfrac{{{m_1}{m_2}}}{{{d^2}}}$. To remove this proportionality he introduced the constant G. ${F_{grav}} = G\dfrac{{{m_1}{m_2}}}{{{d^2}}}$
(iii) After nearly a century in 1798, Lord Henry Cavendish came to determine the value for that constant G by the experiment of torsional balance.
(vi) Cavendish determined G as $6.75 \times {10^{ - 11}}N{m^2}k{g^{ - 2}}$. Now the accepted value is $6.67 \times {10^{ - 11}}N{m^2}k{g^{ - 2}}$.

Note:
The gravitational force is the weakest of all forces in the universe. It has an appreciable value only if it is between the two objects having large masses.