
The value of
A.
B.
C.
D.
Answer
522.6k+ views
Hint:
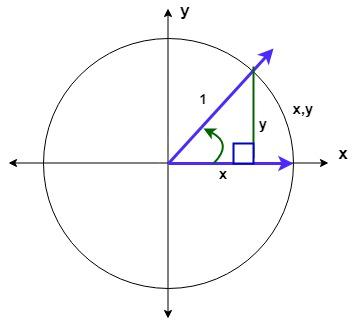
To find out the value of
Complete step-by-step answer:
We know that,
For any right-angled triangle measuring with any of the angles, sine functions equal to the ratio of the length of the opposite side to the length of the hypotenuse side. So, from the figure
Start measuring the angles from the first quadrant and end up with
From the above explanation it is clear that Sin 90 degree equals to the fractional value of
Note: Whenever we come up with the type of problem where we asked to find the value of

To find out the value of
Complete step-by-step answer:
We know that,
For any right-angled triangle measuring with any of the angles, sine functions equal to the ratio of the length of the opposite side to the length of the hypotenuse side. So, from the figure
Start measuring the angles from the first quadrant and end up with
From the above explanation it is clear that Sin 90 degree equals to the fractional value of
Note: Whenever we come up with the type of problem where we asked to find the value of
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




