Question

The $\vec a$ and $\vec b$ are at an angle of $60^\circ $ with each other . Their resultant make an angle of $45^\circ $ with $\vec a$ if $|\vec b|$ = 2 unit then $|\vec a|$ is
A. $\sqrt 3 $
B. $\sqrt 3 - 1$
C. \[\sqrt 3 + 1\]
D. $\sqrt {\dfrac{3}{2}} $

Answer 1

Hint: In order to solve the question, we will use the relation between angle which resultant make with $\vec a$, angle between $\vec a$ and $\vec b$ along with the magnitudes of both vector $\vec a$ and $\vec b$. So as to find the magnitude of the vector $\vec a$ as asked in the question .

Formula used:
$\tan \alpha = \dfrac{{b\sin \theta }}{{a + b\cos \theta }}$
Here, $\theta $ is the angle between the vectors and $\alpha $ is the angle that the vector makes with the resultant.

Complete step by step answer:
In the question we are given the angle between two vector $\vec a$ and $\vec b$ along with this we are also given the angle what resultant make with the $\vec a$ question also provide us the magnitude of vector $\vec b$ and we have to find the magnitude of vector $\vec a$.

Angle between $\vec a$ and $\vec b$ = $60^\circ $
Angle between $\vec a$ and the resultant = $45^\circ $
Magnitude of vector $\vec b$ ( $|\vec b|$ ) = 2 unit

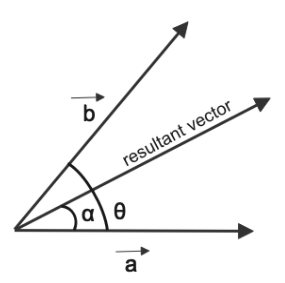
To solve for the magnitude of vector $\vec a$ we only have to use the relation between angle which resultant make with $\vec a$ , angle between $\vec a$ and $\vec b$ along with the magnitudes of both vector $\vec a$ and $\vec b$.
$\tan \alpha = \dfrac{{b\sin \theta }}{{a + b\cos \theta }}$
$\Rightarrow \alpha = 45^\circ $
$\Rightarrow \theta = 60^\circ $

Now we will find the trigonometric values which are required in the formula
$\tan 45^\circ = 1$
$\Rightarrow \sin 60^\circ = \dfrac{{\sqrt 3 }}{2}$
$\Rightarrow \cos 60^\circ = \dfrac{1}{2}$
$\Rightarrow \tan \alpha = \dfrac{{b\sin \theta }}{{a + b\cos \theta }}$
Now we will substitute the trigonometric terms
$\tan 45^\circ = \dfrac{{b\sin 60^\circ }}{{a + b\cos 60^\circ }}$
We will substitute the values of trigonometric terms
$1 = \dfrac{{b\left( {\dfrac{{\sqrt 3 }}{2}} \right)}}{{a + b\left( {\dfrac{1}{2}} \right)}}$
Now we will take the denominator of right hand side to left hand side
$a + b\left( {\dfrac{1}{2}} \right) = b\left( {\dfrac{{\sqrt 3 }}{2}} \right)$
Now substituting the magnitude of vector b
$a + 2\left( {\dfrac{1}{2}} \right) = 2\left( {\dfrac{{\sqrt 3 }}{2}} \right)$
Solving the equation for a and we get
$\therefore a = \sqrt 3 - 1$

Hence, the correct option is B.

Note: Many of the students will make the mistake by not using directly the relationship between angle which resultant make with $\vec a$ , angle between $\vec a$ and $\vec b$ along with the magnitudes of both vector $\vec a$ and $\vec b$ but instead of they will first find the resultant and then they will use trigonometry and diagram to find the result this method have chances of confusion and will make the answer lengthy.