Question

The velocity of the image when the object crosses the mean position and goes towards Q is

A. $A\omega $
B. $-A\omega $
C. $\dfrac{A\omega }{2}$
D. None of the above

Answer 1

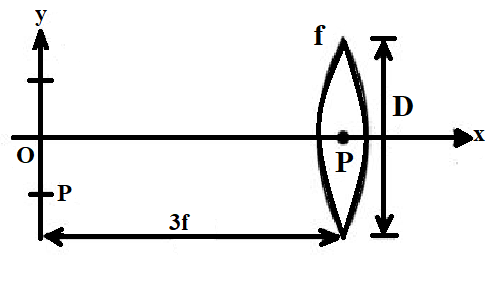
Hint: This is a case of a convex lens. In this situation, the image will be executing the SHM. The object held close to the convex lens of the focal length f, executes SHM between P and Q, O being the mean position. Take x-axis as the main axis of the lens and A < D to answer the following questions.

Formula used:
For solving this question, we will be using the formula for lenses, i.e.,
$\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$

Complete step-by-step answer:
Before solving the given question, let us take a look at all the given parameters,
u = -3f
f = f
Since it’s a convex lens, the sign of the object distance is taken with negative sign
Now,
Applying the lens formula, we have
$\dfrac{1}{v}-\dfrac{1}{u}=\dfrac{1}{f}$
Now, using the given values in the above formula
\[\begin{align}
  & \Rightarrow \dfrac{1}{v}-\dfrac{1}{-3f}=\dfrac{1}{f} \\
\end{align}\]
\[\begin{align}
  & \Rightarrow \dfrac{1}{v}+\dfrac{1}{3f}=\dfrac{1}{f} \\
\end{align}\]
\[\begin{align}
  & \Rightarrow \dfrac{1}{v}=\dfrac{1}{f}-\dfrac{1}{3f} \\
\end{align}\]
\[\Rightarrow \dfrac{1}{v}=\dfrac{2}{3f}\]
So, we have
\[\Rightarrow v=\dfrac{3f}{2}\]
Now, using the formula for the magnification
$m=\dfrac{h'}{h}=\dfrac{v}{u}$
$\Rightarrow m=\dfrac{\dfrac{3f}{2}}{-3f}$
$\Rightarrow m=-\dfrac{1}{2}$
So, we can say that image will be inverted and have a path difference of $\pi $
SHM will be executed by the image in this case,
$\Rightarrow y=\dfrac{A}{2}\sin (\omega t+\pi )$
On differentiating with respect to time
\[\Rightarrow v=\dfrac{dy}{dt}=\dfrac{A\omega }{2}\cos (\omega t+\pi )\]
When the image crosses the mean position, t = 0
So, velocity at that time will be
$\Rightarrow v=\dfrac{A\omega }{2}\cos \pi $
$\Rightarrow v=-\dfrac{A\omega }{2}$
Therefore, The velocity of the image when the object crosses the mean position and goes towards Q will be $-\dfrac{A\omega }{2}$

So, the correct answer is “Option D”.

Note: You can see that the velocity of an object executing SHM can be given by the expression,
\[\Rightarrow v=\dfrac{A\omega }{2}\cos (\omega t+\pi )\]
This formula will be useful in solving many such questions with ease.