Question

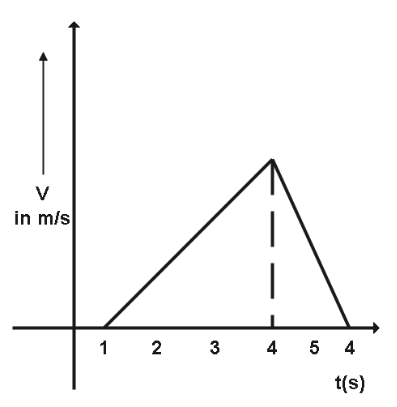
The velocity time graph of a car is as shown in the figure above. Find the acceleration and deceleration of the car if its total displacement is $ 90m $ .

Answer 1

Hint: To solve this question, one must know about the concept of what a velocity-time graph says and if we have to calculate the acceleration, what we have to do. Here firstly we will calculate the area of the graph and then as per question when the graph is moving upwards that is acceleration and coming downward is the acceleration.

Complete Step By Step Answer:
According to the question we have the given displacement i.e., $ 90m $ .
And to find the displacement we will simply find the area under the curve.
And we know that area of a triangle is given by, $ \dfrac{1}{2} \times b \times h $ ,
Where,
 $ b $ is the base and
 $ h $ is the height.
And it is given that the base is $ 5 $ and
Let us assume $ v $ be the base.
Therefore, the area of the triangle is $ \dfrac{1}{2} \times 5 \times v = 2.5v $ i.e., also displacement.
So, $
  2.5v = 90 \\
   \Rightarrow v = 36 \\
  $
Now, we have found the velocity and now we have to calculate the acceleration and deceleration.
In the above graph we can see that the car is accelerating in time-period $ 1 $ to $ 4 $ and decelerating in $ 4 $ to $ 6 $ .
And we know acceleration is given by velocity upon time.
Therefore, acceleration of the car is $ \dfrac{v}{t} = \dfrac{{36}}{3} = 12m{\text{ }}{s^{ - 2}} $ and
Deceleration is $ \dfrac{v}{t} = \dfrac{{36}}{2} = 18m{\text{ }}{s^{ - 2}} $
Hence the acceleration and deceleration of the car is $ 12m{\text{ }}{s^{ - 2}} $ and $ 18m{\text{ }}{s^{ - 2}} $ respectively.

Note:
Note the following points and remember. Velocity as well as displacement both are vector quantities whereas the speed and distance both are scalar quantities. Also note that the area under the velocity-time graph gives us the distance travelled by the body in a certain time frame. And the acceleration of the velocity-time graph is given by the slope.