Question

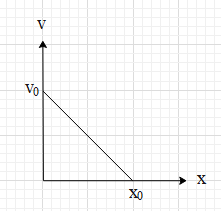
The velocity-displacement graph of a particle moving along a straight line is shown. The most suitable acceleration-displacement graph will be
  

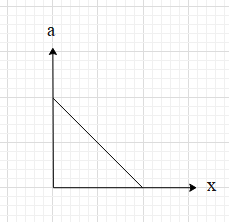
A.

B.

C.

D.

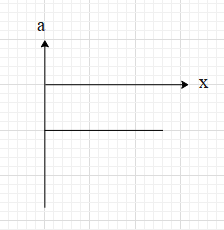
Answer 1

Hint: First find the equation of the straight line to derive a relation between the particle’s velocity and displacement. Then differentiate it to get an expression for the acceleration. After this analyse the equation and obtain a relation between acceleration and displacement.

Formula used:
$\dfrac{dv}{dt}=a$
$\dfrac{dx}{dt}=v$

Complete step by step answer:
Let us analyse the given graph of the velocity-displacement graph and understand the relation between the velocity and the displacement of the particle. We can do this by deriving the equation of the curve.
In the given graph, we can see that the curve is a straight line. The equation of a straight can be written in form $y=mx+c$ ….. (i),
where y, x are the coordinates of the Cartesian plane, m is the slope of the line and c is the y intercept of the line.
In this case, the y coordinate is the velocity of the particle and the x coordinate is the displacement of the particles. Therefore, $y=v$.
We can see that the y intercept is ${{v}_{0}}$. This means that $c={{v}_{0}}$.
Here, the line is making an obtuse angle with the positive x-axis. Therefore, the slope of the line will be negative and its value will be $m=-\dfrac{{{v}_{0}}}{{{x}_{0}}}$.
Substitute the values y, m and c in (i).
$\Rightarrow v=-\dfrac{{{v}_{0}}}{{{x}_{0}}}x+{{v}_{0}}$ ….. (ii).
Hence, we found the equation of the curve.
Now, differentiate (ii) with respect to time t.
 $\Rightarrow \dfrac{dv}{dt}=-\dfrac{{{v}_{0}}}{{{x}_{0}}}\dfrac{dx}{dt}+0$.
But, derivative of velocity with respect to time is acceleration, i.e. $\dfrac{dv}{dt}=a$.
And also derivative of displacement with respect to time is velocity, i.e. $\dfrac{dx}{dt}=v$.
Therefore,
$\Rightarrow a=-\dfrac{{{v}_{0}}}{{{x}_{0}}}v$
Substitute the value of v from (ii).
$\Rightarrow a=-\dfrac{{{v}_{0}}}{{{x}_{0}}}\left( -\dfrac{{{v}_{0}}}{{{x}_{0}}}x+{{v}_{0}} \right)$.
$\Rightarrow a={{\left( \dfrac{{{v}_{0}}}{{{x}_{0}}} \right)}^{2}}x+\left( \dfrac{-v_{0}^{2}}{{{x}_{0}}} \right)$ …. (iii).
Even equation (iii) is in the form of $y=mx+c$,
where $y=a$, $m={{\left( \dfrac{{{v}_{0}}}{{{x}_{0}}} \right)}^{2}}$ and $c=-\dfrac{v_{0}^{2}}{{{x}_{0}}}$.
This means that m is positive and c is negative.
Therefore, the graph of the acceleration-displacement graph is a straight line with a positive slope and a negative y intercept.
Thus, the most suitable graph from the options is graph B.

So, the correct answer is “Option B”.

Note:
Some students may make the following mistakes. They may think that the velocity is decreasing as the particles displace further and since the velocity is decreasing, its acceleration will be negative. However, acceleration is the rate of change of velocity with respect to time and not with respect to displacement of the particle.
Hence, this logic will be incorrect.