Question

The vibrations of four air columns are represented in the figure. The ratio of frequencies np : nq : nr : ns is

A. 12 : 6 : 3 : 5
B. 1 : 2 : 4 : 3
C. 4 : 2 : 3 : 1
D. 6 : 2 : 3 : 4

Answer 1

Hint: In the case of the closed end air column, the wavelength to be considered will be 4 times the length of the column, whereas, in the case of the open end air column, the wavelength to be considered will be 2 times the length of the column, while calculating the frequencies.

Formula used:
\[n=\dfrac{v}{4l}\]
\[n=\dfrac{v}{2l}\]

Complete step by step answer:
The air column p represents the fundamental closed end.
Thus the frequency of the air column p is given as,
\[{{n}_{p}}=\dfrac{v}{4l}\]

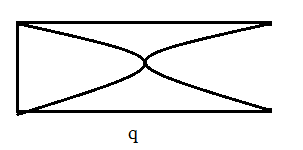
The air column q represents the fundamental open end.
Thus the frequency of the air column q is given as,
\[{{n}_{q}}=\dfrac{v}{2l}\]

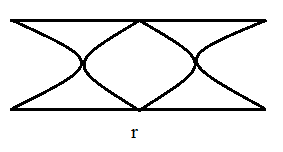
The air column r represents the second overtone open end.
Thus the frequency of the air column r is given as,
\[\begin{align}
  & {{n}_{r}}=\dfrac{2v}{2l} \\
 & {{n}_{r}}=\dfrac{v}{l} \\
\end{align}\]

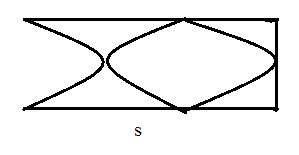
The air column s represents the second overtone closed end.
Thus the frequency of the air column s is given as,
\[{{n}_{s}}=\dfrac{3v}{4l}\]

The ratio of the frequencies of the air columns p, q, r and s is given as follows:
\[{{n}_{p}}:{{n}_{q}}:{{n}_{r}}:{{n}_{s}}=\dfrac{1}{4}:\dfrac{1}{2}:1:\dfrac{3}{4}\]
Multiply by 4 to take the LCM.
Therefore, the ratio of the frequencies is,
\[{{n}_{p}}:{{n}_{q}}:{{n}_{r}}:{{n}_{s}}=1:2:4:3\]

As, the ratio of frequencies np : nq : nr : ns of four air columns is 1 : 2 : 4 : 3, thus option (B) 1 : 2 : 4 : 3 is correct.

Note:
The things to be on your finger-tips for further information on solving these types of problems are: The frequencies should be calculated considering open end and the closed end concepts.