Question

The volume and area of the curved surface of the right circular cylinder is $1540{{m}^{3}}$ and $440{{m}^{2}}$ respectively. Then find the radius of base and height of the cylinder.

Answer 1

Hint: Now we know that the curved surface area of right circular cylinder is given by $\pi {{r}^{2}}h$ and the curved surface of right circular cylinder is given by $2\pi rh$ . Hence using this we will get two equations in r and h. we will solve them simultaneously to find r and h.

Complete step by step answer:
Now consider a right circular cylinder

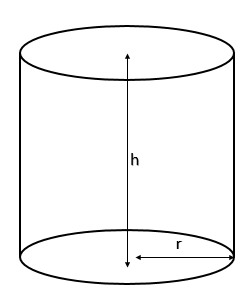
We know that the Volume of curved right circular cylinder is given by formula $\pi {{r}^{2}}h$ where r is the radius of the cylinder and h is the height of the cylinder.
Now the volume of cylinder is given as $1540{{m}^{3}}$
Hence we have $\pi {{r}^{2}}h=1540{{m}^{3}}$
Let this be called equation (1)
$\pi {{r}^{2}}h=1540{{m}^{3}}.........................\left( 1 \right)$
Now we also have formula for curved surface area of cylinder which is $2\pi rh$
Also the curved surface area is given to be $440{{m}^{2}}$
Hence we have $2\pi rh=440$
Let this be called equation (2)
$2\pi rh=440{{m}^{2}}..............\left( 2 \right)$
Now let us divide equation (1) by equation (2). Hence we will get
$\dfrac{\pi {{r}^{2}}h}{2\pi rh}=\dfrac{1540}{440}$
Now cancelling the common terms we get $\dfrac{r}{2}=\dfrac{1540}{440}$
Now if we divide 1540 and 440 by 220 and hence we get
$\dfrac{r}{2}=\dfrac{7}{2}$
Now multiplying the whole equation by 2 we get r = 7
Hence r = 7m
Now substituting r = 7 in equation (2) we get
$2\pi \left( 7 \right)h=440$
Now for simplicity let us take $\pi =\dfrac{22}{7}$
Hence we have
$\begin{align}
  & 2\times \dfrac{22}{7}\times 7\times h=440 \\
 & \Rightarrow 2\times 22\times h=440 \\
 & \Rightarrow 44\times h=440 \\
 & \Rightarrow h=10 \\
\end{align}$
Hence we get h = 10m

Hence the value of r = 7m and h = 10m.

Note: Note that the curved surface area and total surface area are different for the cylinder. Curved surface area of the cylinder is given by $2\pi rh$ and total surface area is given by $2\pi rh+2\pi {{r}^{2}}$ . Also note that $\pi $ is an irrational number and cannot be expressed in the form of $\dfrac{p}{q}$ for simplicity we take it as $\dfrac{22}{7}$.