Question

The volume of solid right cylinder cones is 4928cu.cm. If a height is 24cm, then find the radius of the cone. \[\left( Take\ \pi =\dfrac{22}{7} \right)\]

Answer 1

Hint: For the above question we will have to use the formula of volume of a solid right cylinder cone having radius r and height ‘h’ given by,
\[volume\ of\ cone=\dfrac{1}{3}\pi {{r}^{2}}h\]
Where \[\pi \]is a constant and approx. value is $3.14\ or\ \dfrac{22}{7}$.
So, by using the above formula we will get the equation in variable ‘r’ and solving it we will get the value of ‘r’ i.e. radius.

Complete step-by-step answer:
We have been given that the volume of the solid right cylinder cone is 4928cu.cm and the height is 24cm and we have been asked to find the radius of that cone.
Let, the radius be ‘r’ cm.

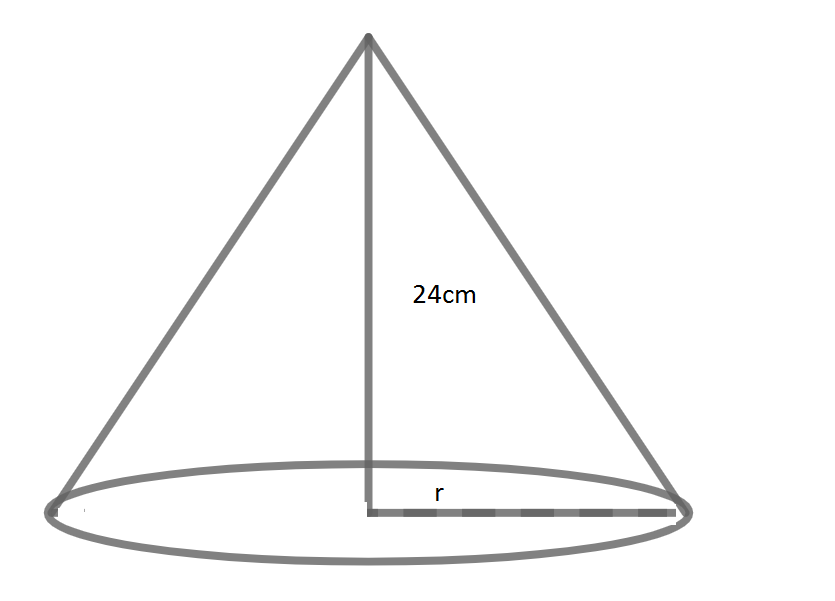
We know that volume of a cone having radius ‘r’ and height ‘h’ is given by,
\[\begin{align}
  & V=\dfrac{1}{3}\pi {{r}^{2}}h \\
 & \Rightarrow \dfrac{1}{3}\pi {{r}^{2}}h=4928 \\
 & \Rightarrow \dfrac{1}{3}\pi {{r}^{2}}\times 24=4928 \\
\end{align}\]
As, we have been given \[\pi =\dfrac{22}{7}\].
\[\begin{align}
  & \Rightarrow \dfrac{1}{3}\times \dfrac{22}{7}\times {{r}^{2}}\times 24=4928 \\
 & \Rightarrow {{r}^{2}}=\dfrac{4928\times 3\times 7}{22\times 24} \\
 & \Rightarrow {{r}^{2}}=196 \\
\end{align}\]
Taking square root, we get,
\[\begin{align}
  & \Rightarrow \sqrt{{{r}^{2}}}=\sqrt{196} \\
 & \Rightarrow r=14cm \\
\end{align}\]
Therefore, the radius of the cone is 14cm.

Note: Be careful while substituting the value of \[\pi \] in the equation. Don’t use the value of \[\pi \] as 3.14. Since, we have been given to take \[\pi \] as \[\dfrac{22}{7}\]. So, if you will \[\pi \] as 3.14 you will not get the exact answer instead of that you will get an approximate value.
Also, remember that sometimes by mistake we use the formula for volume of cones as \[\pi {{r}^{2}}h\] which is for a cylinder and will give us the wrong answer.