Answer
460.8k+ views
Hint
We know that Newton's second law states that a net force acting on an object causes the object to accelerate in the direction of the force. The third law can be understood this way for every action force, there is an equal and opposite reaction force. The net force is the vector sum of all the forces that act upon an object. That is to say, the net is the sum of all the forces, taking into account the fact that a force is a vector and two forces of equal magnitude and opposite direction will cancel each other out.
Complete step by step answer
We know that the net force reaction is:
Where,
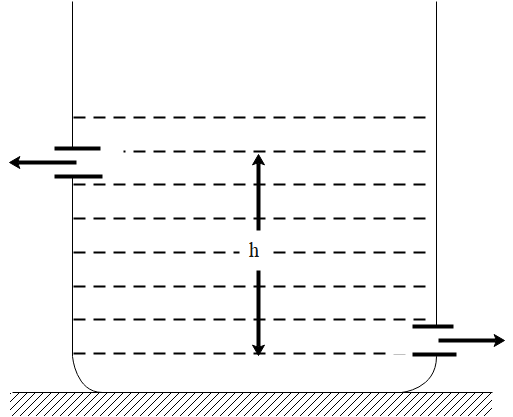
$ \text{F}={{\text{F}}_{\text{B}}}-{{\text{F}}_{\text{A}}}=\dfrac{\text{d}{{\rho }_{\text{B}}}}{\text{dt}}-\dfrac{\text{d}{{\rho }_{\text{A}}}}{\text{dt}} $
$ ={{\operatorname{av}}_{\text{B}}}\rho \times {{\text{v}}_{\text{B}}}-{{\operatorname{av}}_{\text{A}}}\rho \times {{\text{v}}_{\text{A}}} $
$ \rho $ is the density, $ v $ is the velocity, $ F $ is force, $ a $ is area, $ h $ is height.
Therefore, we can derive the equation of net force.
$ \therefore \text{F}=\operatorname{ap}\left( \text{v}_{\text{B}}^{2}-\text{v}_{\text{A}}^{2} \right)\ldots \ldots (i) $
According to Bernoulli’s theorem,
$ {{\rho }_{\text{A}}}+\dfrac{1}{2}\rho \text{v}_{\text{A}}^{2}+\text{pgh}={{\rho }_{\text{B}}}+\dfrac{1}{2}\rho \text{v}_{\text{B}}^{2}+0 $
$ \Rightarrow \dfrac{1}{2}\rho \left( \text{v}_{\text{B}}^{2}-\text{v}_{\text{A}}^{2} \right)=\rho \text{gh} $
$ \Rightarrow \text{v}_{\text{B}}^{2}-\text{v}_{\text{A}}^{2}=2\text{gh}\ldots \ldots \text{(ii)} $
From the given equations (i) and (ii), we get the equation,
$ \text{F}=\operatorname{a}\rho (2\text{gh})=2\text{a}\rho \text{gh} $
Therefore, the correct answer is Option (C).
Note
We know that Bernoulli’s theorem states that within a horizontal flow of fluid, points of higher speed will have less pressure than points of slower fluid speed. We can say that the sum of pressure energy, kinetic energy, and potential energy per unit mass of an incompressible, non-viscous fluid in a streamlined flow remains constant. For example, this principle explains why airplane wings are curved along the top and why ships have to steer away from each other as they pass. The pressure above the wing is lower than below it, providing life from underneath the wing.
We know that Newton's second law states that a net force acting on an object causes the object to accelerate in the direction of the force. The third law can be understood this way for every action force, there is an equal and opposite reaction force. The net force is the vector sum of all the forces that act upon an object. That is to say, the net is the sum of all the forces, taking into account the fact that a force is a vector and two forces of equal magnitude and opposite direction will cancel each other out.
Complete step by step answer
We know that the net force reaction is:
Where,
$ \text{F}={{\text{F}}_{\text{B}}}-{{\text{F}}_{\text{A}}}=\dfrac{\text{d}{{\rho }_{\text{B}}}}{\text{dt}}-\dfrac{\text{d}{{\rho }_{\text{A}}}}{\text{dt}} $
$ ={{\operatorname{av}}_{\text{B}}}\rho \times {{\text{v}}_{\text{B}}}-{{\operatorname{av}}_{\text{A}}}\rho \times {{\text{v}}_{\text{A}}} $
$ \rho $ is the density, $ v $ is the velocity, $ F $ is force, $ a $ is area, $ h $ is height.
Therefore, we can derive the equation of net force.
$ \therefore \text{F}=\operatorname{ap}\left( \text{v}_{\text{B}}^{2}-\text{v}_{\text{A}}^{2} \right)\ldots \ldots (i) $
According to Bernoulli’s theorem,
$ {{\rho }_{\text{A}}}+\dfrac{1}{2}\rho \text{v}_{\text{A}}^{2}+\text{pgh}={{\rho }_{\text{B}}}+\dfrac{1}{2}\rho \text{v}_{\text{B}}^{2}+0 $
$ \Rightarrow \dfrac{1}{2}\rho \left( \text{v}_{\text{B}}^{2}-\text{v}_{\text{A}}^{2} \right)=\rho \text{gh} $
$ \Rightarrow \text{v}_{\text{B}}^{2}-\text{v}_{\text{A}}^{2}=2\text{gh}\ldots \ldots \text{(ii)} $
From the given equations (i) and (ii), we get the equation,
$ \text{F}=\operatorname{a}\rho (2\text{gh})=2\text{a}\rho \text{gh} $
Therefore, the correct answer is Option (C).
Note
We know that Bernoulli’s theorem states that within a horizontal flow of fluid, points of higher speed will have less pressure than points of slower fluid speed. We can say that the sum of pressure energy, kinetic energy, and potential energy per unit mass of an incompressible, non-viscous fluid in a streamlined flow remains constant. For example, this principle explains why airplane wings are curved along the top and why ships have to steer away from each other as they pass. The pressure above the wing is lower than below it, providing life from underneath the wing.
Recently Updated Pages
Fill in the blanks with suitable prepositions Break class 10 english CBSE

Fill in the blanks with suitable articles Tribune is class 10 english CBSE

Rearrange the following words and phrases to form a class 10 english CBSE

Select the opposite of the given word Permit aGive class 10 english CBSE

Fill in the blank with the most appropriate option class 10 english CBSE

Some places have oneline notices Which option is a class 10 english CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

How do you graph the function fx 4x class 9 maths CBSE

Which are the Top 10 Largest Countries of the World?

What is the definite integral of zero a constant b class 12 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Define the term system surroundings open system closed class 11 chemistry CBSE

Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE