Question

Three circles touch each other externally. If the tangents at their points of contact meet at a point whose distance from a point of contact is 4, then find the ratio of product of the sum of the radii of the circles, is
A. 2:1
B. 4:1
C. 8:1
D. 16:1

Answer 1

Hint: Use the Heron’s formula to find the area of the triangle. The perimeter of a triangle is double the perimeter of the triangle. In this question the distance of the point of contact is given as 4 and as we know the inradius of a triangle is given as $ Inradius $ = $ \dfrac{{Area}}{{Semiperimeter}} $ , hence by substituting the values we will find the ratio of product of the sum of the radii of the circles.

Complete answer:
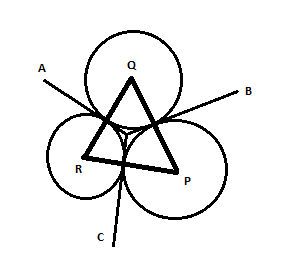
Let us name the centers of the three circles as P, Q and R, respectively and let their respective radii be p, q and r.
Also, the common tangents meet at points A, B and C and all the 3 tangents meet at O.
From the question we know that, $ OA\; = \,OB\; = OC = 4 $ units.
Now, if we draw a circle by keeping the center of the circle at O and $ OA,OB,OC $ being equal (equal to 4 units), point O will also be the incenter of the $ \vartriangle ABC $ .
Thus, the inradius of the $ \Delta ABC $ is 4 units.
We know that, $ Inradius $ = $ \dfrac{{Area}}{{Semiperimeter}} $
⇒ $ r = \dfrac{\vartriangle }{s} $ $ .....(i) $

We know that, Perimeter of the triangle = 2× semi perimeter
  $
  2s = p + q + q + r + r + p \\
   \Rightarrow s = \dfrac{{(2p + 2q + 2r)}}{2} \\
   \Rightarrow s = p + q + r \\
   $
By Heron’s Formula,
 \[
  \vartriangle = \sqrt {s(s - a)(s - b)(s - c)} = \sqrt {(p + q + r)(r)(q)(p)} ......(ii) \\
    \\
  \therefore From\;eq(i)\;\& eq(ii), \\
  4 = \dfrac{{\sqrt {(p + q + r)(r)(q)(p)} }}{{(p + q + r)}} \\
   \Rightarrow 16 = \dfrac{{(p + q + r)(r)(q)(p)}}{{{{(p + q + r)}^2}}} \\
   \Rightarrow 16 = \dfrac{{pqr}}{{p + q + r}} \\
 \]
Therefore, the ratio of the product of radii of the circles to the sum of the radii of the circles is 16:1.
Option D is correct.

Note: Heron’s formula to find the area of the triangle requires the length of all sides of the triangle which is one of the demerits of this formula so to us this formula we need to find all the sides of the triangle but this formula can give the area of the triangle without the measurements of the angles of the triangle.