Question

Three consecutive vertices of a parallelogram are $\left( {1, - 2} \right)$, $\left( {3,6} \right)$ and $\left( {5,10} \right)$. The coordinates of the fourth vertex are
A.$\left( { - 3,2} \right)$
B.$\left( {2, - 3} \right)$
C.$\left( {3,2} \right)$
D.$\left( { - 2, - 3} \right)$

Answer 1

Hint: Here we need to find the coordinate of the fourth vertex of the parallelogram. We will use the coordinates of the fourth vertex of the parallelogram to be any variable. We will use the property of the parallelogram that both the diagonals of a parallelogram bisect each other. So we will first find the point of intersection of the two diagonals by finding the midpoint of the both the pair of diagonal vertices individually. Then we will equate both the midpoint as they are the same point. From there, we will get the value of the variable and hence, the required coordinates of the fourth vertex.

Complete step-by-step answer:
Here we need to find the coordinate of the fourth vertex of the parallelogram. It is given that the three consecutive vertices of a parallelogram are $\left( {1, - 2} \right)$, $\left( {3,6} \right)$ and $\left( {5,10} \right)$.
Let the fourth vertex of the paralegal be $\left( {x,y} \right)$
So we will first draw the figure of the parallelogram using the vertices of the parallelogram.

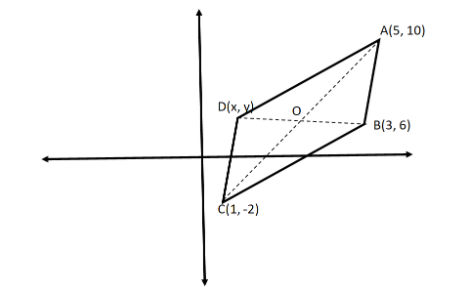
We know that both the diagonals of a parallelogram bisect each other. So we will first midpoint i.e. point $O$ of the vertices $A\left( {5,10} \right)$ and $C\left( {1, - 2} \right)$.
$x$ Coordinate of point $O$ $ = \dfrac{{5 + 1}}{2}$
On adding the numbers, we get
$ \Rightarrow $ $x$ coordinate of point $O$ $ = \dfrac{6}{2}$
On further simplification, we get
$ \Rightarrow $ $x$ coordinate of point $O$ $ = 3$
Now, we will find the $y$ coordinate of the point $O$.
$y$ coordinate of point $O$ $ = \dfrac{{10 + \left( { - 2} \right)}}{2}$
On adding the numbers, we get
$ \Rightarrow $ $y$ coordinate of point $O$ $ = \dfrac{8}{2}$
On further simplification, we get
$ \Rightarrow $ $y$ coordinate of point $O$ $ = 4$
We can got the point $O$ as $\left( {3,4} \right)$ …………… $\left( 1 \right)$
Now, we will again find the midpoint i.e. point $O$ of the points $D\left( {x,y} \right)$ and $B\left( {3,6} \right)$.
$x$ coordinate of point $O$ $ = \dfrac{{x + 3}}{2}$
Now, we will find the $y$ coordinate of the point $O$
$y$ coordinate of point $O$ $ = \dfrac{{y + 6}}{2}$
Therefore, we have got point $O$ as $\left( {\dfrac{{x + 3}}{2},\dfrac{{y + 6}}{2}} \right)$.
But we have already obtained the value of coordinates of point $O$ in equation 1.
So we will equate the coordinates of the point $O$.
On equation the $x$ coordinate of point $O$, we get
$3 = \dfrac{{x + 3}}{2}$
On cross multiplying the terms, we get
$ \Rightarrow 6 = x + 3$
Now, we will subtract 3 from both sides.
$ \Rightarrow 6 - 3 = x + 3 - 3$
Subtracting the like terms, we get
$ \Rightarrow x = 3$
On equation the $y$ coordinate of point $O$, we get
$4 = \dfrac{{y + 6}}{2}$
On cross multiplying the terms, we get
$ \Rightarrow 8 = y + 6$
Now, we will subtract 6 from both sides.
$ \Rightarrow 8 - 6 = y + 6 - 6$
Subtracting the like terms, we get
$ \Rightarrow y = 2$
Therefore, point $D$ i.e. the fourth vertex of the parallelogram is $\left( {3,2} \right)$.
Hence, the correct option is option C.

Note: Here we have obtained the fourth vertex of the parallelogram. A parallelogram is defined as the quadrilateral whose opposite sides are parallel to each and also the opposite sides are equal in length. Also remember that both the diagonals of a parallelogram bisect each other and we have used the same properties of the parallelogram to get the required point.