
Three equal cubes are placed adjacently in a row. Find the ratio of the total surface area of the resulting cuboid to the sum of the total surface areas of the three cubes.
(a) 7: 13
(b) 7: 3
(c) 7: 9
(d) 7: 5
Answer
481.8k+ views
Hint: Here, we need to find the ratio of the total surface area of the resulting cuboid to the sum of the total surface areas of the three cubes. First, we will find the sum of the surface area of the three cubes. Then, we need to find the dimensions of the resulting cuboid when the three cubes are joined end to end. Then, we will use the formula for total surface area of a cuboid and then, calculate the ratio of the total surface area of the resulting cuboid to the sum of the total surface areas of the three cubes.
Formula used:
We will use the following formulas:
1.The total surface area of a cube is given by the formula
2.The total surface area of a cuboid is given by the formula
Complete step-by-step answer:
First, we will find the total surface areas of the three cubes.
It is given that the three cubes are equal.
Therefore, the volume, area, and edge of the cubes are the same.
Let the length of the side of the cubes be
The total surface area of a cube is given by the formula
Substituting
Total surface area of 1 cube
Thus, we get
Total surface area of the other two cubes
Now, we will find the sum of the total surface areas of the three cubes.
The sum of the total surface areas of the three cubes
Adding the like terms of the expression, we get
The sum of the total surface areas of the three cubes
Now, let us draw the diagram to show how the resulting cuboid looks.
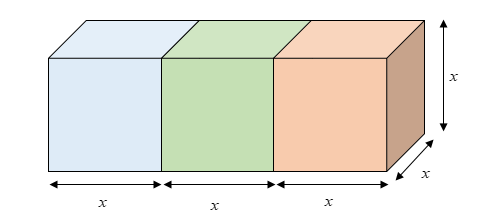
We can observe that when the three cubes are joined together end to end, the breadth and height of the resulting cuboid is equal to the side of the cubes, that is
The length of the cuboid is the sum of the lengths of the sides of the three cubes.
Therefore, the length of the cuboid
Adding the like terms, we get
Now, we will find the total surface area of the resulting cuboid.
The total surface area of a cuboid is given by the formula
Substituting
Total surface area of the resulting cuboid
Multiplying the terms in the parentheses, we get
Adding the like terms in the parentheses, we get
Multiplying 2 by 7, we get
Finally, we will find the ratio of the total surface area of the resulting cuboid to the sum of the total surface areas of the three cubes.
Dividing the total surface area of the cuboid by the sum of the total surface areas of the three cubes, we get
Simplifying the expression, we get
Therefore, the ratio of the total surface area of the resulting cuboid to the sum of the total surface areas of the three cubes is 7: 9.
Thus, the correct option is option (c).
Note: We need to remember that the sum of the surface areas of the three cubes will not be equal to the surface area of the resulting cuboid, unlike volume.
We added the like terms in the solution. Like terms are the terms whose variables and their exponents are the same. For example,
Formula used:
We will use the following formulas:
1.The total surface area of a cube is given by the formula
2.The total surface area of a cuboid is given by the formula
Complete step-by-step answer:
First, we will find the total surface areas of the three cubes.
It is given that the three cubes are equal.
Therefore, the volume, area, and edge of the cubes are the same.
Let the length of the side of the cubes be
The total surface area of a cube is given by the formula
Substituting
Total surface area of 1 cube
Thus, we get
Total surface area of the other two cubes
Now, we will find the sum of the total surface areas of the three cubes.
The sum of the total surface areas of the three cubes
Adding the like terms of the expression, we get
The sum of the total surface areas of the three cubes
Now, let us draw the diagram to show how the resulting cuboid looks.

We can observe that when the three cubes are joined together end to end, the breadth and height of the resulting cuboid is equal to the side of the cubes, that is
The length of the cuboid is the sum of the lengths of the sides of the three cubes.
Therefore, the length of the cuboid
Adding the like terms, we get
Now, we will find the total surface area of the resulting cuboid.
The total surface area of a cuboid is given by the formula
Substituting
Total surface area of the resulting cuboid
Multiplying the terms in the parentheses, we get
Adding the like terms in the parentheses, we get
Multiplying 2 by 7, we get
Finally, we will find the ratio of the total surface area of the resulting cuboid to the sum of the total surface areas of the three cubes.
Dividing the total surface area of the cuboid by the sum of the total surface areas of the three cubes, we get
Simplifying the expression, we get
Therefore, the ratio of the total surface area of the resulting cuboid to the sum of the total surface areas of the three cubes is 7: 9.
Thus, the correct option is option (c).
Note: We need to remember that the sum of the surface areas of the three cubes will not be equal to the surface area of the resulting cuboid, unlike volume.
We added the like terms in the solution. Like terms are the terms whose variables and their exponents are the same. For example,
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Trending doubts
Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

The southernmost point of the Indian mainland is known class 7 social studies CBSE

Convert 200 Million dollars in rupees class 7 maths CBSE

How many crores make 10 million class 7 maths CBSE

Write a pair of integers whose sum gives i Zero ii class 7 maths CBSE

List of coprime numbers from 1 to 100 class 7 maths CBSE





