Question

Three forces are acting on a body as shown in the figure. To have the resultant force only along the Y-direction, the magnitude of the minimum additional force needed along OX is?

Answer 1

Hint: We have been given the forces and the angle they make with the axes. Using this we can find the value of resultant along both the axes. But we want resultant only in Y –direction so the sum of the forces will be zero along X – axis so that the resultant along X direction also becomes zero

Complete step by step answer:
If we want the resultant of all the given forces making respective given forces with the axes to be only in Y – direction then the components of all the forces along X – axis will be zero so that the resultant in X direction becomes zero.
The forces along X and Y axes are given by the product of force with the cos (along X – axis) and sine (along Y – axis) of the angles formed between the force and the axes respectively.
The angles formed along X – axis to find the value of forces along the same can be given as:

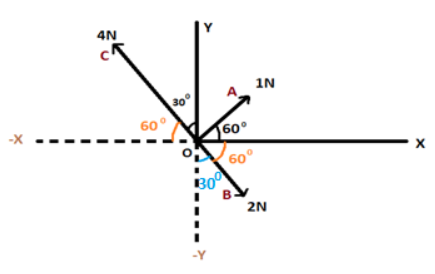
$\angle - YOB = {30^\circ }$ as it is vertically opposite to the given angle of 30°
$\angle XOB = {60^o}$
$\left(
\because \angle XO - Y = {90^\circ } \\
\Rightarrow \angle XOB + \angle - YOB = {90^\circ } \\
\Rightarrow \angle XOB + {30^\circ } = {90^\circ } \\
\Rightarrow \angle XOB = {60^\circ } \\ \right)$
Similarly, $\angle - XOC = {60^o}$
Now, the magnitude of all the forces along X – axis can be given as:
$
{F_A} = 1 \times \cos {60^\circ } \\
{F_B} = 2 \times \cos {60^\circ } \\
{F_C} = 4 \times \cos {60^\circ } \\
 $
The value of $\cos {60^\circ }$ is $\dfrac{1}{2}$, so:
$
{F_A} \to 1 \times \dfrac{1}{2} = \dfrac{1}{2}N \\
{F_B} \to 2 \times \dfrac{1}{2} = 1N \\
{F_C} \to 4 \times \dfrac{1}{2} = - 2N \\
 $
As the force C is in the negative direction of X – axis, its value is taken as negative.
Let the minimum additional force required along OX (X – axis) be ${F_{req}}$.
Then the sum of all forces equated to zero is given as:
$
\dfrac{1}{2}N + 1N - 2N + {F_{req}} = 0 \\
\dfrac{3}{2}N - 2N + {F_{req}} = 0 \\
\Rightarrow {F_{req}} = 2N - \dfrac{3}{2}N \\
\Rightarrow {F_{req}} = \dfrac{1}{2}N \\
 or \\
 \Rightarrow {F_{req}} = 0.5N \\
 $

Therefore, the minimum additional force needed along OX is $\dfrac{1}{2}N$ or 0.5 N

Note:
Remember that we have to consider sine of angle for Y – axis and cos of angle for X – axis.
The resultant initially would have been along both X and Y directions but it was given in the question that we need resultant along the y – direction only. Thus for neglecting the components of force along the X direction, we equated their sum along with the required force (since it was also along X – axis) to zero.