Question

Three identical bodies of equal mass $M$ each are moving along a circle of radius R under the action of their mutual gravitational attraction. The speed of each body is: -
A) $\sqrt {\dfrac{{GM}}{R}} $
B) $\sqrt {\dfrac{{GM}}{{3R}}} $
C) $\sqrt {\dfrac{{GM}}{{\sqrt 3 R}}} $
D) $\sqrt {\dfrac{{GM}}{{\sqrt 2 R}}} $

Answer 1

Hint:Here each particle experiences a force of attraction from the other two bodies. Find the direction of the resultant force on a body due to the presence of other two bodies. Also calculate the value of this resultant force. As the three bodies are moving in a circle, the force of attraction on each particle must be directed towards the center of the circle.

Complete step-by-step solution:In this problem, we are given three bodies which are moving in a circle. As a result, we can say that the bodies are placed on the sides of an equilateral triangle. And the circle is known as circumcircle. We know that for a triangle with a circumcircle, the centroid and the circumcenter coincide. Let us represent it diagrammatically.

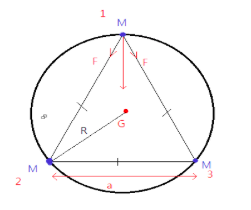
Here, the three bodies are having equal masses, $G$ is the centroid, $a$ is the length of the side of the equilateral triangle, $R$ is the radius of the circle.
From trigonometry, we have
$a = \sqrt 3 R$ --equation $1$
As the bodies are identical and we have achieved that the distances between two bodies must be equal therefore, the forces acting on the three bodies must also be equal.
Let us consider the forces acting on the body at point $1$ , the resultant force on this body will be towards the centre. The magnitude of this force ${F_1}$ due bodies at point $2$ and $3$ will be

${F_1} = {F_2} + {F_3}$

Force at point one due body at point two is

$ \Rightarrow {F_{1,2}} = \dfrac{{G{M^2}}}{{{a^2}}}$

Force at point one due body at point three is

$ \Rightarrow {F_{1,3}} = \dfrac{{G{M^2}}}{{{a^2}}}$

Resultant force is given by

$F = \sqrt {\left| {{F_{1,2}}} \right| + \left| {{F_{1,3}}} \right| + \left| {{F_{1,2}}} \right|\left| {{F_{1,3}}} \right|\cos {{60}^ \circ }} $

Since the triangle is equilateral hence the angle is ${60^ \circ }$

$ \Rightarrow F = \sqrt {\dfrac{{G{M^2}}}{{{a^2}}} + \dfrac{{G{M^2}}}{{{a^2}}} + 2\dfrac{{G{M^2}}}{{{a^2}}} \times \dfrac{{G{M^2}}}{{{a^2}}} \times \dfrac{1}{2}} $
$ \Rightarrow F = \sqrt {3\dfrac{{G{M^2}}}{{{a^2}}}} $
$ \Rightarrow F = \sqrt 3 \dfrac{{G{M^2}}}{{{a^2}}}$

Since the particle is moving in a circle, hence centripetal force is also acting on it and the centripetal force must be equal to the magnitude of the force acting on each body.

$ \Rightarrow \dfrac{{M{v^2}}}{R} = \sqrt 3 \dfrac{{G{M^2}}}{{{a^2}}}$

Here $v$ is the speed of the body.

Substituting $a = \sqrt 3 R$ from equation $1$ , we get

$ \Rightarrow \dfrac{{M{v^2}}}{R} = \sqrt 3 \dfrac{{G{M^2}}}{{3{R^2}}}$
$ \Rightarrow v = \sqrt {\dfrac{{GM}}{{\sqrt 3 R}}} $

This is the speed of each body.

Thus, option C is the correct option.

Note: The bodies were identical therefore the forces acting on the three bodies were also equal. Remember that for a triangle with circumcircle, the centroid and the circumcentre coincide. Don’t forget to account for the centripetal force and remember that the centripetal force must be balanced with the forces acting by other bodies.