Question

Three identical Styrofoam balls each of mass $ 10g $ are suspended from a fixed point by three non-conducting threads, each with a length of $ 1m $ and negligible mass. At equilibrium, the three balls form an equilateral triangle with sides of $ 10cm $ . If the common charge on each ball is $ n \times {10^{ - 8}}C $ , then find $ n $ .

Answer 1

Hint :To solve this question, we will first draw the diagram of the given situation. We know that each charge experiences two repelling forces by the other two charges. First we will find this force and then equate it and the weight of the balls with the horizontal and vertical components of tension.

Complete Step By Step Answer:
Let us first draw the diagram for the given situation.

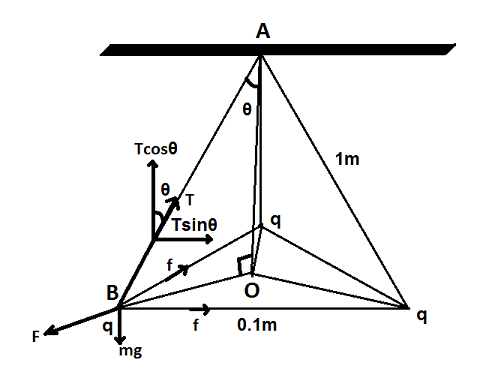
Let $ f $ be the repelling force of two other balls acting on the charge of the ball as shown in the diagram.
As it is given that the three balls form an equilateral triangle, the angle between these two forces will be $ {60^ \circ } $ . Thus, the resultant force is given by:
 $ F = \sqrt {{f^2} + {f^2} + 2{f^2}\cos 60} = \sqrt {3{f^2}} = \sqrt 3 f $
Now, let us consider triangle AOB. We can write
 $ \tan \theta = \dfrac{{OB}}{{OA}} $
We know that for equilateral triangles the distance of the vertex to its centroid will be $ \dfrac{1}{{\sqrt 3 }} $ times its side. Therefore, $ OB = \dfrac{{0.1}}{{\sqrt 3 }}m $ .
OA will be the length of the thread which is given as $ 1m $ .
 $ \Rightarrow \tan \theta = \dfrac{{0.1}}{{\sqrt 3 }} $
We can see from the figure that tension and repelling force, both are in the same plane.
We will equate the horizontal and vertical forces acting on one of the charges for equilibrium condition as shown in the diagram.
 $
   \Rightarrow T\sin \theta = F \\
   \Rightarrow T\sin \theta = \sqrt 3 f \\
  $
and
 $ \Rightarrow T\cos \theta = mg $
We are given $ m = 10g = {10^{ - 2}}kg $ and we will take $ g = 10m/{s^2} $
 $ \Rightarrow T\cos \theta = {10^{ - 2}} \times 10 = {10^{ - 1}} = 0.1 $
Now we will decide both this equation.
 $
   \Rightarrow \dfrac{{T\sin \theta }}{{T\cos \theta }} = \dfrac{{\sqrt 3 f}}{{0.1}} \\
   \Rightarrow \tan \theta = \dfrac{{\sqrt 3 f}}{{0.1}} \\
  $
We have already determined that $ \tan \theta = \dfrac{{0.1}}{{\sqrt 3 }} $ .
 $
   \Rightarrow \dfrac{{0.1}}{{\sqrt 3 }} = \dfrac{{\sqrt 3 f}}{{0.1}} \\
   \Rightarrow f = \dfrac{{{{10}^{ - 2}}}}{3} \\
  $
We know that the force between two similar charges is given by
 $ f = \dfrac{{k{q^2}}}{{{l^2}}} $ , where , $ k $ is the constant whose value is $ 9 \times {10^9} $ , $ q $ is the charge and $ l $ is the distance between two charges. Therefore, we can write
 $
   \Rightarrow {q^2} = \dfrac{{f{l^2}}}{k} \\
   \Rightarrow {q^2} = \dfrac{{{{10}^{ - 2}} \times {{10}^{ - 2}}}}{{3 \times 9 \times {{10}^9}}} \\
   \Rightarrow {q^2} = 0.0370 \times {10^{ - 13}} \\
   \Rightarrow {q^2} = 37 \times {10^{ - 16}} \\
   \Rightarrow q = 6.08 \times {10^{ - 8}}C \\
  $
We are given that the common charge on each ball is $ n \times {10^{ - 8}}C $ .
Therefore $ n = 6.08 $ .

Note :
In this question, the most important step is to draw the diagram carefully. This is because we will know the directions of forces properly by doing this. The consideration of the plane in which the forces are acting is very important to determine the correct answer.