Answer
432.6k+ views
Hint:The figure shows three plates connected together which can be broken into two capacitors. The plates of the capacitors are connected with each other; this means that they are connected in parallel. In parallel, the potential drop on the capacitors is the same. Using formula for capacitance we can find a relation between change and capacitance and from the distance between plates, we can determine the relation between both capacitors and then calculate charge.
Formulas used:
$C=\dfrac{Q}{V}$
$\dfrac{{{q}_{1}}}{{{C}_{1}}}=\dfrac{{{q}_{2}}}{{{C}_{2}}}$
$C=\dfrac{{{\varepsilon }_{0}}A}{d}$
$\dfrac{{{C}_{1}}}{{{C}_{2}}}=\dfrac{{{d}_{2}}}{{{d}_{1}}}$
Complete answer:
Capacitors are devices which store charge on them. Their ability to store charge is represented by capacitance. It is calculated as
$C=\dfrac{Q}{V}$ - (1)
Here, $C$ is the capacitance
$Q$ is the charge
$V$ is the potential difference
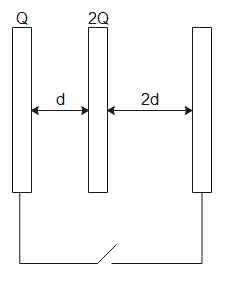
The above plates can be divided into two capacitors as shown
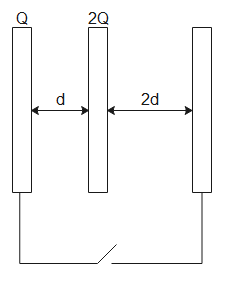
As we can see, both plates of the two capacitors are connected together; this means that they are connected in parallel. The potential difference is the same in parallel combination. Therefore,
${{V}_{1}}={{V}_{2}}$
From eq (1),
$\dfrac{{{q}_{1}}}{{{C}_{1}}}=\dfrac{{{q}_{2}}}{{{C}_{2}}}$ - (2)
The capacitance of a parallel plate capacitor depends on the dimensions of the capacitor as-
$C=\dfrac{{{\varepsilon }_{0}}A}{d}$ - (3)
Here, ${{\varepsilon }_{0}}$ is the permittivity of free space
$A$ is the area of cross section between the plates
$d$ is the distance between the plates
${{\varepsilon }_{0}}$ and $A$ are constants, therefore, form eq (3),
$\dfrac{{{C}_{1}}}{{{C}_{2}}}=\dfrac{{{d}_{2}}}{{{d}_{1}}}$
Substituting values from the figure in the above equation, we get,
$\dfrac{{{C}_{1}}}{{{C}_{2}}}=\dfrac{2d}{d}$
$\Rightarrow {{C}_{1}}=2{{C}_{2}}$ - (4)
Substituting eq (4) in eq (2), we get,
$\begin{align}
& \dfrac{{{q}_{1}}}{{{C}_{1}}}=\dfrac{{{q}_{2}}}{{{C}_{2}}} \\
& \Rightarrow \dfrac{{{q}_{1}}}{2{{C}_{2}}}=\dfrac{{{q}_{2}}}{{{C}_{2}}} \\
& \therefore {{q}_{1}}=2{{q}_{2}} \\
\end{align}$
We know that,
$\begin{align}
& {{q}_{1}}+{{q}_{2}}=2Q \\
& \Rightarrow 2{{q}_{2}}+{{q}_{2}}=2Q \\
& \Rightarrow 3{{q}_{2}}=2Q \\
& \therefore {{q}_{2}}=\dfrac{2Q}{3} \\
\end{align}$
${{q}_{2}}$has the value ${{q}_{2}}=\dfrac{2Q}{3}$, therefore, ${{q}_{1}}$ will have the value-
$\begin{align}
& {{q}_{1}}=2{{q}_{2}} \\
& \Rightarrow {{q}_{1}}=2\times \dfrac{2Q}{3} \\
& \therefore {{q}_{1}}=\dfrac{4Q}{3} \\
\end{align}$
Therefore, the charge on the first capacitor is $\dfrac{2Q}{3}$ and the charge on the second capacitor is $\dfrac{4Q}{3}$.
The charge that flows through the wire can key is closed is
$\begin{align}
& -{{q}_{2}}-(-{{q}_{1}}) \\
& \Rightarrow \dfrac{-4Q}{3}+\dfrac{2Q}{3}=-\dfrac{2Q}{3} \\
\end{align}$
Therefore, the charge that flows through the wire is $\dfrac{2Q}{3}$.
Hence, the correct option is (D).
Note:
The negative charge on the charge that flows through the circuit indicates that this charge flows opposite to the flow of current. In series, the charge is the same on the capacitors, while in parallel, the potential drop on capacitors is the same. The permittivity of a material is its ability to store electrical energy in an electric field.
Formulas used:
$C=\dfrac{Q}{V}$
$\dfrac{{{q}_{1}}}{{{C}_{1}}}=\dfrac{{{q}_{2}}}{{{C}_{2}}}$
$C=\dfrac{{{\varepsilon }_{0}}A}{d}$
$\dfrac{{{C}_{1}}}{{{C}_{2}}}=\dfrac{{{d}_{2}}}{{{d}_{1}}}$
Complete answer:
Capacitors are devices which store charge on them. Their ability to store charge is represented by capacitance. It is calculated as
$C=\dfrac{Q}{V}$ - (1)
Here, $C$ is the capacitance
$Q$ is the charge
$V$ is the potential difference

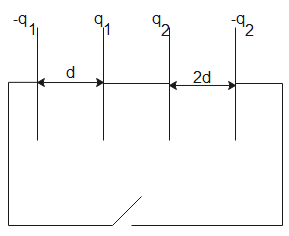
The above plates can be divided into two capacitors as shown

As we can see, both plates of the two capacitors are connected together; this means that they are connected in parallel. The potential difference is the same in parallel combination. Therefore,
${{V}_{1}}={{V}_{2}}$
From eq (1),
$\dfrac{{{q}_{1}}}{{{C}_{1}}}=\dfrac{{{q}_{2}}}{{{C}_{2}}}$ - (2)
The capacitance of a parallel plate capacitor depends on the dimensions of the capacitor as-
$C=\dfrac{{{\varepsilon }_{0}}A}{d}$ - (3)
Here, ${{\varepsilon }_{0}}$ is the permittivity of free space
$A$ is the area of cross section between the plates
$d$ is the distance between the plates
${{\varepsilon }_{0}}$ and $A$ are constants, therefore, form eq (3),
$\dfrac{{{C}_{1}}}{{{C}_{2}}}=\dfrac{{{d}_{2}}}{{{d}_{1}}}$
Substituting values from the figure in the above equation, we get,
$\dfrac{{{C}_{1}}}{{{C}_{2}}}=\dfrac{2d}{d}$
$\Rightarrow {{C}_{1}}=2{{C}_{2}}$ - (4)
Substituting eq (4) in eq (2), we get,
$\begin{align}
& \dfrac{{{q}_{1}}}{{{C}_{1}}}=\dfrac{{{q}_{2}}}{{{C}_{2}}} \\
& \Rightarrow \dfrac{{{q}_{1}}}{2{{C}_{2}}}=\dfrac{{{q}_{2}}}{{{C}_{2}}} \\
& \therefore {{q}_{1}}=2{{q}_{2}} \\
\end{align}$
We know that,
$\begin{align}
& {{q}_{1}}+{{q}_{2}}=2Q \\
& \Rightarrow 2{{q}_{2}}+{{q}_{2}}=2Q \\
& \Rightarrow 3{{q}_{2}}=2Q \\
& \therefore {{q}_{2}}=\dfrac{2Q}{3} \\
\end{align}$
${{q}_{2}}$has the value ${{q}_{2}}=\dfrac{2Q}{3}$, therefore, ${{q}_{1}}$ will have the value-
$\begin{align}
& {{q}_{1}}=2{{q}_{2}} \\
& \Rightarrow {{q}_{1}}=2\times \dfrac{2Q}{3} \\
& \therefore {{q}_{1}}=\dfrac{4Q}{3} \\
\end{align}$
Therefore, the charge on the first capacitor is $\dfrac{2Q}{3}$ and the charge on the second capacitor is $\dfrac{4Q}{3}$.
The charge that flows through the wire can key is closed is
$\begin{align}
& -{{q}_{2}}-(-{{q}_{1}}) \\
& \Rightarrow \dfrac{-4Q}{3}+\dfrac{2Q}{3}=-\dfrac{2Q}{3} \\
\end{align}$
Therefore, the charge that flows through the wire is $\dfrac{2Q}{3}$.
Hence, the correct option is (D).
Note:
The negative charge on the charge that flows through the circuit indicates that this charge flows opposite to the flow of current. In series, the charge is the same on the capacitors, while in parallel, the potential drop on capacitors is the same. The permittivity of a material is its ability to store electrical energy in an electric field.
Recently Updated Pages
10 Examples of Evaporation in Daily Life with Explanations

10 Examples of Diffusion in Everyday Life

1 g of dry green algae absorb 47 times 10 3 moles of class 11 chemistry CBSE

What is the meaning of celestial class 10 social science CBSE

What causes groundwater depletion How can it be re class 10 chemistry CBSE

Under which different types can the following changes class 10 physics CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Which are the Top 10 Largest Countries of the World?

How do you graph the function fx 4x class 9 maths CBSE

Who was the leader of the Bolshevik Party A Leon Trotsky class 9 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Which is the largest saltwater lake in India A Chilika class 8 social science CBSE

Ghatikas during the period of Satavahanas were aHospitals class 6 social science CBSE